题目内容
3.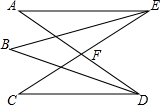 如图,EC与AD相交于F,EB、DB平分∠AEC、∠ADC交于点B.
如图,EC与AD相交于F,EB、DB平分∠AEC、∠ADC交于点B.(1)请问:∠B与∠A、∠C之间有何关系?直接写出结论即可,不需证明;
(2)如果∠A:∠B:∠C=2:4:a,求a的值.
分析 (1)令BE与AD交于G,由三角形内角和定理得出∠A+∠AEB=∠B+∠ADB,∠C+∠CDB=∠B+∠BEC,由角平分线的性质得出∠AEB=∠BEC,∠CDB=∠ADB,故可得出结论;
(2)根据∠A:∠B:∠C=2:4:a可令∠A=2,∠B=4,则∠C=a,代入(1)中的关系式即可得出结论.
解答 解:(1)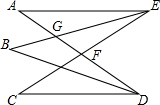 令BE与AD交于G.
令BE与AD交于G.
∵△AGE中,∠A+∠AEB+∠AGE=180°,∠B+∠ADB+∠BGD=180°,∠AGE=∠BGD,
∴∠A+∠AEB=∠B+∠ADB.
同理:∠C+∠CDB=∠B+∠BEC,
∴∠A+∠C+∠AEB+∠CDB=2∠B+∠ADB+∠BEC.
∵EB平分∠AEC,
∴∠AEB=∠BEC.
∵DB平分∠ADC,
∴∠CDB=∠ADB,
∴∠A+∠C=2∠B.
(2)∵∠A:∠B:∠C=2:4:a,
∴令∠A=2,∠B=4,则∠C=a.
∵由(1)知,∠A+∠C=2∠B,
∴2+a=8,解得a=6.
点评 本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
相关题目
11.下列计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | $\sqrt{12}$-$\sqrt{3}$=$\sqrt{3}$ | C. | $\sqrt{8}$÷$\sqrt{2}$=4 | D. | $\sqrt{(-5)^{2}}$=-5 |
15.(-2)3等于( )
| A. | -8 | B. | 8 | C. | -6 | D. | 9 |
12.⊙O的直径为2,圆心O到直线l的距离是方程x2-2x+1=0的根,则⊙O与直线l的位置关系是( )
| A. | 相切 | B. | 相离 | C. | 相交 | D. | 相切或相交 |
 如果点A,B,C,D所对应的数为a,b,c,d,在a,b,c,d的大小关系是b<d<c<a.
如果点A,B,C,D所对应的数为a,b,c,d,在a,b,c,d的大小关系是b<d<c<a.
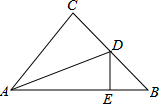 如图,三角形ABC中,∠C=90°,∠BAC的平分线交BC于D,DE⊥AB于E,已知CD=3,BD=5,求三角形ABC的周长.
如图,三角形ABC中,∠C=90°,∠BAC的平分线交BC于D,DE⊥AB于E,已知CD=3,BD=5,求三角形ABC的周长.