题目内容
4.已知锐角A满足关系式2sin2A-7sinA+3=0,求sinA的值.分析 由等式可得(sinA-3)(2sinA-1)=0,即sinA-3=0或2sinA-1=0,解得sinA=3或sinA=$\frac{1}{2}$,根据锐角三角函数值的取值范围可得答案.
解答 解:∵2sin2A-7sinA+3=0,
∴(sinA-3)(2sinA-1)=0,
则sinA-3=0或2sinA-1=0,
解得:sinA=3(舍)或sinA=$\frac{1}{2}$,
∴sinA=$\frac{1}{2}$.
点评 本题主要考查因式分解法解一元二次方程和锐角三角函数值,根据方程的特点选择合适的方法是解题的关键.

练习册系列答案
相关题目
15.下列图形中(如图),∠1和∠2是同位角的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.下列线段中,不可能是同一个三角形的三边上的高的是( )
| A. | 1cm,1cm,2cm | B. | 2cm,2cm,1cm | C. | 2cm,3cm,3cm | D. | 3cm,4cm,6cm |
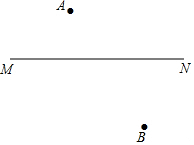 A、B为直线MN外两点,且在MN异侧,A、B到MN的距离不相等,试求一点P,满足下条件:
A、B为直线MN外两点,且在MN异侧,A、B到MN的距离不相等,试求一点P,满足下条件:
 如图,在正方形ABCD和正方形CEFG中,点B、C、E在同一条直线上,点M是边AD的中点,已知AB=a,CE=b(a<b).
如图,在正方形ABCD和正方形CEFG中,点B、C、E在同一条直线上,点M是边AD的中点,已知AB=a,CE=b(a<b). 如图,过x轴上一点A作平行于y轴的直线分别与抛物线y=$\frac{1}{4}$x2及y=x2交于B、C两点,若正方形BCDE的一边DE与y轴重合,则此正方形BCDE的面积为$\frac{16}{9}$.
如图,过x轴上一点A作平行于y轴的直线分别与抛物线y=$\frac{1}{4}$x2及y=x2交于B、C两点,若正方形BCDE的一边DE与y轴重合,则此正方形BCDE的面积为$\frac{16}{9}$.