题目内容
18.已知圆锥的侧面积为15π,母线长5,则圆锥的高为 .
.
分析 设圆锥的底面圆的半径为r,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形面积公式得到$\frac{1}{2}$•2π•r•5=15π,然后解方程求出r后利用勾股定理计算圆锥的高.
解答 解:设圆锥的底面圆的半径为r,
根据题意得$\frac{1}{2}$•2π•r•5=15π,解得r=3,
所以圆锥的高=$\sqrt{{5}^{2}-{3}^{2}}$=4.
故答案为4.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
相关题目
13.已知A(1,1)、B(3,2),点B绕点A逆时针旋转90°到达点C处,则点C的坐标是( )
| A. | (0,3) | B. | (-1,3) | C. | (3,-1) | D. | (3,0) |
3.下列运算正确的是( )
| A. | $\sqrt{2+3}$=$\sqrt{2}$+$\sqrt{3}$ | B. | (-$\sqrt{3}$)2=3 | C. | 3a-a=3 | D. | (a2)3=a5 |
8.与$\sqrt{5}$最接近的整数是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
 如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.求证:AB=CD.
如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.求证:AB=CD.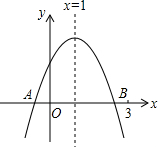 如图,二次函数y=ax2+bx+c的图象交x轴于A、B两点,下列结论:
如图,二次函数y=ax2+bx+c的图象交x轴于A、B两点,下列结论: