题目内容
9.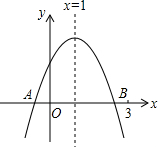 如图,二次函数y=ax2+bx+c的图象交x轴于A、B两点,下列结论:
如图,二次函数y=ax2+bx+c的图象交x轴于A、B两点,下列结论:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a-b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2;⑥OA•OB=$\frac{c}{a}$;
其中正确的有( )
| A. | 3个 | B. | 2个 | C. | 4个 | D. | 5个 |
分析 根据抛物线开口方向得a<0,由抛物线对称轴为直线x=-$\frac{b}{2a}$=1,得到b=-2a>0,即2a+b=0,由抛物线与y轴的交点位置得到c>0,所以abc<0;根据二次函数的性质得当x=1时,函数有最大值a+b+c,则当m≠1时,a+b+c>am2+bm+c,即a+b>am2+bm;根据抛物线的对称性得到抛物线与x轴的另一个交点在(-1,0)的右侧,则当x=-1时,y<0,所以a-b+c<0;把ax12+bx1=ax22+bx2先移项,再分解因式得到(x1-x2)[a(x1+x2)+b]=0,而x1≠x2,则a(x1+x2)+b=0,即x1+x2=-$\frac{b}{a}$,然后把b=-2a代入计算得到x1+x2=2;设A(x1,0),B(x2,0),根据抛物线和方程的关系得出x1•x2=$\frac{c}{a}$,即可求得OA•OB=-x1•x2=-$\frac{c}{a}$.
解答 解:∵抛物线开口向下,
∴a<0,
∵抛物线对称轴为直线x=-$\frac{b}{2a}$=1,
∴b=-2a>0,即2a+b=0,所以②正确;
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,所以①错误;
∵抛物线对称轴为直线x=1,
∴函数的最大值为a+b+c,
∴当m≠1时,a+b+c>am2+bm+c,即a+b>am2+bm,所以③正确;
∵抛物线与x轴的一个交点在(3,0)的左侧,而对称轴为直线x=1,
∴抛物线与x轴的另一个交点在(-1,0)的右侧
∴当x=-1时,y<0,
∴a-b+c<0,所以④错误;
∵ax12+bx1=ax22+bx2,
∴ax12+bx1-ax22-bx2=0,
∴a(x1+x2)(x1-x2)+b(x1-x2)=0,
∴(x1-x2)[a(x1+x2)+b]=0,
而x1≠x2,
∴a(x1+x2)+b=0,即x1+x2=-$\frac{b}{a}$,
∵b=-2a,
∴x1+x2=2,所以⑤正确;
设A(x1,0),B(x2,0),
∴x1•x2=$\frac{c}{a}$.
∵OA=-x1,OB=x2,
∴OA•OB=-x1•x2=-$\frac{c}{a}$,所以⑥错误.
故选:A.
点评 本题考查了二次函数图象与系数的关系:二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线开口向上;当a<0时,抛物线开口向下;一次项系数b和二次项系数a共同决定对称轴的位置,当a与b同号时(即ab>0),对称轴在y轴左侧;当a与b异号时(即ab<0),对称轴在y轴右侧;常数项c决定抛物线与y轴交点.抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定,△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

| A. | y=2(x+2)2 | B. | y=2(x-2)2 | C. | y=2x2+2 | D. | y=2x2-2 |
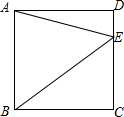 如图,点E在正方形ABCD的边CD上,若△ABE的面积为18,CE=4,则线段BE的长为2$\sqrt{13}$.
如图,点E在正方形ABCD的边CD上,若△ABE的面积为18,CE=4,则线段BE的长为2$\sqrt{13}$.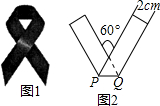 红丝带(图1)是对HIV和艾滋病认识的国际符号,1991年在美国纽约第一次出现,它代表了关心,这一标志被越来越多的人佩带,用来表示他们对HIV和艾滋病的关心.现将宽为2cm的长方形纸条折叠成如图2所示的丝带形状,那么折痕PQ的长是$\frac{4\sqrt{3}}{3}$.
红丝带(图1)是对HIV和艾滋病认识的国际符号,1991年在美国纽约第一次出现,它代表了关心,这一标志被越来越多的人佩带,用来表示他们对HIV和艾滋病的关心.现将宽为2cm的长方形纸条折叠成如图2所示的丝带形状,那么折痕PQ的长是$\frac{4\sqrt{3}}{3}$. .
.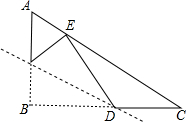 如图,在Rt△ABC中,∠ABC=90°,AC=10,BC=8,点D是线段BC上一点,DC=3,沿过点D的直线折叠三角形,使点B落在斜边AC所在直线上,点B的对应点E到点A的距离是$\frac{38}{5}$-$\frac{2\sqrt{138}}{5}$.
如图,在Rt△ABC中,∠ABC=90°,AC=10,BC=8,点D是线段BC上一点,DC=3,沿过点D的直线折叠三角形,使点B落在斜边AC所在直线上,点B的对应点E到点A的距离是$\frac{38}{5}$-$\frac{2\sqrt{138}}{5}$.