题目内容
10.先化简,再求值:($\frac{a}{a-b}$-1)÷$\frac{b}{{a}^{2}{-b}^{2}}$,其中a=2cos30°+1,b=2sin60°-1.分析 先根据分式混合运算的法则把原式进行化简,再求出a、b的值代入进行计算即可.
解答 解:原式=$\frac{a-a+b}{a-b}$•$\frac{(a-b)(a+b)}{b}$
=$\frac{b}{a-b}$•$\frac{(a-b)(a+b)}{b}$
=a+b,
当a=2cos30°+1=2×$\frac{\sqrt{3}}{2}$+1=$\sqrt{3}$+1,b=2sin60°-1=2×$\frac{\sqrt{3}}{2}$-1=$\sqrt{3}$-1时,
原式=$\sqrt{3}$+1+$\sqrt{3}$-1=2$\sqrt{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
15.某商品原价每件x元,后来店主将每件增加10元,再降价25%,则现在的单价(元)是( )
| A. | 25%x+10 | B. | (1-25%)x+10 | C. | 25%(x+10) | D. | (1-25%)(x+10) |
2.化简$\frac{{x}^{2}-25}{{x}^{2}-5x}$-1结果正确的是( )
| A. | $\frac{x+5}{x}$ | B. | $\frac{x-5}{x}$ | C. | $\frac{5}{x}$ | D. | $\frac{x}{x-5}$ |
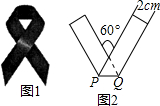 红丝带(图1)是对HIV和艾滋病认识的国际符号,1991年在美国纽约第一次出现,它代表了关心,这一标志被越来越多的人佩带,用来表示他们对HIV和艾滋病的关心.现将宽为2cm的长方形纸条折叠成如图2所示的丝带形状,那么折痕PQ的长是$\frac{4\sqrt{3}}{3}$.
红丝带(图1)是对HIV和艾滋病认识的国际符号,1991年在美国纽约第一次出现,它代表了关心,这一标志被越来越多的人佩带,用来表示他们对HIV和艾滋病的关心.现将宽为2cm的长方形纸条折叠成如图2所示的丝带形状,那么折痕PQ的长是$\frac{4\sqrt{3}}{3}$. .
.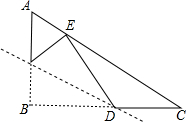 如图,在Rt△ABC中,∠ABC=90°,AC=10,BC=8,点D是线段BC上一点,DC=3,沿过点D的直线折叠三角形,使点B落在斜边AC所在直线上,点B的对应点E到点A的距离是$\frac{38}{5}$-$\frac{2\sqrt{138}}{5}$.
如图,在Rt△ABC中,∠ABC=90°,AC=10,BC=8,点D是线段BC上一点,DC=3,沿过点D的直线折叠三角形,使点B落在斜边AC所在直线上,点B的对应点E到点A的距离是$\frac{38}{5}$-$\frac{2\sqrt{138}}{5}$.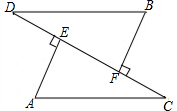 已知,AC=BD,AE⊥DC于E,BF⊥DC于F,AE=BF.求证:DE=CF.
已知,AC=BD,AE⊥DC于E,BF⊥DC于F,AE=BF.求证:DE=CF.