题目内容
6.汽车租赁行业现在火爆起来.小明开办了一家汽车租赁公司,拥有汽车20辆,在旺季每辆车的每天租金为600元时,可全部租出:当每辆车的每天租金增加50元时,未租出的车将增加一辆,租出的车辆每辆每天需要维护费200元,未租出的车辆每辆每天需要维护费100元,每天其他开销共计1000元.(1)当每辆车的租金为1000元时,每天能租出多少辆车?每天净收益为多少元?
(2)当每辆车的每天租金定为多少元时,租赁公司的每天净收益最大?最大净收益为多少元?(每天净收益=总租金-租出去车辆维护费-未租出去车辆维护费-每天其他开销)
分析 (1)根据:租出的车=20-$\frac{现在租金-原定租金}{50}$,每天净收益=总租金-租出去车辆维护费-未租出去车辆维护费-每天其他开销,列式计算可得;
(2)根据:每天净收益=总租金-租出去车辆维护费-未租出去车辆维护费-每天其他开销列出函数关系式,根据二次函数性质可得最值情况.
解答 解:(1)当每辆车的租金为x元时,每天租出的车有:20-$\frac{1000-600}{50}$=12(辆),
每天的净收益为:12×(1000-200)-8×100-1000=7800元,
答:当每辆车的租金为1000元时,每天能租出12辆车,每天净收益为7800元.
(2)设每辆车每天的租金为x元,每天的净收益为y元,根据题意,
得:y=(x-200)(20-$\frac{x-600}{50}$)-$\frac{x-600}{50}$×100-1000
=-$\frac{1}{50}$x2+34x-6200,
∵a=-$\frac{1}{50}$<0,
∴当x=-$\frac{34}{2×(-\frac{1}{50})}$=850元时,y取得最大值8250元,
答:当每辆车的每天租金定为850元时,租赁公司的每天净收益最大,最大净收益为8250元.
点评 本题主要考查二次函数的实际应用能力,根据题意理清数量间关系是根本,根据相等关系列出函数关系式是关键.

练习册系列答案
相关题目
16.在正三角形、平行四边形、矩形、菱形和圆这五个图形中,既是轴对称图形又是中心对称图形有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
14.将二次函数y=2x2的图象向右平移2个单位,得到该二次函数的表达式是( )
| A. | y=2(x+2)2 | B. | y=2(x-2)2 | C. | y=2x2+2 | D. | y=2x2-2 |
11.下列运算正确的是( )
| A. | (a+b)2=a2+b2 | B. | $\sqrt{a^2+b^2}$=$\sqrt{a^2}$+$\sqrt{b^2}$ | C. | a2•a3=a5 | D. | $\sqrt{{a}^{4}}$=±a2 |
15.某商品原价每件x元,后来店主将每件增加10元,再降价25%,则现在的单价(元)是( )
| A. | 25%x+10 | B. | (1-25%)x+10 | C. | 25%(x+10) | D. | (1-25%)(x+10) |
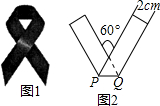 红丝带(图1)是对HIV和艾滋病认识的国际符号,1991年在美国纽约第一次出现,它代表了关心,这一标志被越来越多的人佩带,用来表示他们对HIV和艾滋病的关心.现将宽为2cm的长方形纸条折叠成如图2所示的丝带形状,那么折痕PQ的长是$\frac{4\sqrt{3}}{3}$.
红丝带(图1)是对HIV和艾滋病认识的国际符号,1991年在美国纽约第一次出现,它代表了关心,这一标志被越来越多的人佩带,用来表示他们对HIV和艾滋病的关心.现将宽为2cm的长方形纸条折叠成如图2所示的丝带形状,那么折痕PQ的长是$\frac{4\sqrt{3}}{3}$. .
.