题目内容
18. 如图,⊙O的直径CD垂直于弦AB,垂足为E,F为DC延长线上一点,且∠CBF=∠CDB.
如图,⊙O的直径CD垂直于弦AB,垂足为E,F为DC延长线上一点,且∠CBF=∠CDB.(1)求证:FB为⊙O的切线;
(2)若AB=8,CE=2,求⊙O的半径.
分析 (1)连接OB,根据圆周角定理证得∠CBD=90°,然后根据等边对等角以及等量代换,证得∠OBF=90°即可证得;
(2)首先利用垂径定理求得BE的长,根据勾股定理得出方程,即可求得圆的半径.
解答 (1)证明:连接OB,如图所示:
∵CD是直径,
∴∠CBD=90°,
又∵OB=OD,
∴∠OBD=∠D,
又∠CBF=∠D,
∴∠CBF=∠OBD,
∴∠CBF+∠OBC=∠OBD+∠OBC,
∴∠OBF=∠CBD=90°,即OB⊥BF,
∴FB为⊙O的切线;
(2)解:∵CD是圆的直径,CD⊥AB,
∴BE=$\frac{1}{2}$AB=4,
设圆的半径是R,
在直角△OEB中,根据勾股定理得:R2=(R-2)2+42,
解得:R=5,
即⊙O的半径为5.
点评 本题考查了切线的判定,圆周角定理,勾股定理;熟练掌握切线的判定定理,由勾股定理得出方程是解决问题(2)的关键.

练习册系列答案
相关题目
7.下列不属于二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}x+y=3\\ x-y=1\end{array}$ | B. | $\left\{\begin{array}{l}x=3\\ x-y=1\end{array}$ | C. | $\left\{\begin{array}{l}x+y=3\\ y=1\end{array}$ | D. | $\left\{\begin{array}{l}xy=3\\ x-y=1\end{array}$ |

 如图,平行四边形ABCD的对角线AC、BD相交于点O,点E是CD的中点.△ABD的周长为8cm,则△DOE的周长是4cm.
如图,平行四边形ABCD的对角线AC、BD相交于点O,点E是CD的中点.△ABD的周长为8cm,则△DOE的周长是4cm.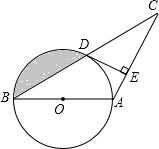 已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E.
已知:如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E. 如图,在平行四边形ABCD中,以点A为圆心,一定长为半径作圆弧,分别交AD、AB于点E、F;再分别以点E、F为圆心,大于$\frac{1}{2}$EF长为半径作圆弧,两弧交于点G;作射线AG,交边CD于点H,若AB=6,AD=4,则四边形ABCH的周长与三角形ADH的周长之差为4.
如图,在平行四边形ABCD中,以点A为圆心,一定长为半径作圆弧,分别交AD、AB于点E、F;再分别以点E、F为圆心,大于$\frac{1}{2}$EF长为半径作圆弧,两弧交于点G;作射线AG,交边CD于点H,若AB=6,AD=4,则四边形ABCH的周长与三角形ADH的周长之差为4. 如图,在?ABCD中,∠ADC的平分线交AB于点E,∠ABC的平分线交CD于点F,求证:四边形EBFD是平行四边形.
如图,在?ABCD中,∠ADC的平分线交AB于点E,∠ABC的平分线交CD于点F,求证:四边形EBFD是平行四边形.