题目内容
14.已知一次函数y=kx+1与$y=-\frac{1}{2}x+b$的图象相交于点(2,5),求关于x的方程kx+b=0的解.分析 首先将(2,5)点代入一次函数解析式求出k,b的值,进而解方程得出答案.
解答 解:∵一次函数y=kx+1与$y=-\frac{1}{2}x+b$的图象相交于点(2,5),
∴5=2k+1,5=-$\frac{1}{2}$×2+b,
解得:k=2,b=6,
则kx+b=0为:2x+6=0,
解得:x=-3.
点评 此题主要考查了一次函数与一元一次方程,正确得出k,b的值是解题关键.

练习册系列答案
相关题目
7.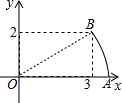 如图,在平面直角坐标系中,点B的坐标为(3,2),以点O为圆心,OB的长为半径画弧,交x轴的正半轴于点A,则点A的横坐标在( )
如图,在平面直角坐标系中,点B的坐标为(3,2),以点O为圆心,OB的长为半径画弧,交x轴的正半轴于点A,则点A的横坐标在( )
 如图,在平面直角坐标系中,点B的坐标为(3,2),以点O为圆心,OB的长为半径画弧,交x轴的正半轴于点A,则点A的横坐标在( )
如图,在平面直角坐标系中,点B的坐标为(3,2),以点O为圆心,OB的长为半径画弧,交x轴的正半轴于点A,则点A的横坐标在( )| A. | 2和3之间 | B. | 3和3.5之间 | C. | 3.5和4之间 | D. | 4和5之间 |
9.估算$\sqrt{6}$的值是在( )
| A. | 1和2之间 | B. | 2和3之间 | C. | 3和4之间 | D. | 4和5之间 |
19.一学生从家去学校每小时走5千米,按原路返回时,每小时走4千米,结果返回的时间比去的时间多用10分钟,设去学校所用的时间为x小时,则正确列出的方程是( )
| A. | 5x=4(x+$\frac{10}{60}$) | B. | 5x=4(x-$\frac{10}{60}$) | C. | 5(x-$\frac{10}{60}$)=4x | D. | 5(x+$\frac{10}{60}$)=4x |
1.某部队第一天行军5h,第二天行军6h,两天共行军120km,且第二天比第一天多走2km,设第一天和第二天行军的速度分别为xkm/h和ykm/h,则符合题意的二元一次方程是( )
| A. | 5x+6y=118 | B. | 5x=6y+2 | C. | 5x=6y-2 | D. | 5(x+2)=6y |