题目内容
6. 如图,以原点O为位似中心,把△OAB放大后得到△OCD,求△OAB与△OCD的相似比.
如图,以原点O为位似中心,把△OAB放大后得到△OCD,求△OAB与△OCD的相似比.
分析 根据点B的坐标和点D的坐标,求出OB=4,OD=6,得出$\frac{OB}{OD}$=$\frac{2}{3}$,再根据△OAB与△OCD关于点O位似,从而求出△OAB与△OCD的相似比.
解答 解:∵点B的坐标是(4,0),点D的坐标是(6,0),
∴OB=4,OD=6,
∴$\frac{OB}{OD}$=$\frac{4}{6}$=$\frac{2}{3}$,
∵△OAB与△OCD关于点O位似,
∴△OAB与△OCD的相似比$\frac{2}{3}$.
点评 此题考查了位似变换,位似变换的两个图形相似.根据相似多边形对应边成比例得OB:OD=2:3.

练习册系列答案
相关题目
16.下列各式能运用公式法进行因式分解的有( )个
(1)-a2+b2
(2)16m2-25n2
(3)9p2-24pq+16q2
(4)(a+b)2+a+b+$\frac{1}{4}$.
(1)-a2+b2
(2)16m2-25n2
(3)9p2-24pq+16q2
(4)(a+b)2+a+b+$\frac{1}{4}$.
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
17.下列根式中,与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{24}$ | B. | $\sqrt{20}$ | C. | $\sqrt{\frac{3}{2}}$ | D. | $\sqrt{18}$ |
14.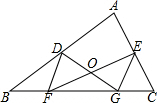 如图,在△ABC中D,E分别是AB,AC的中点,点F,G在BC上,且BC=4BF=4CG,EF与DG相交于点O,若∠DFE=40°,∠DGE=80°,那么∠DOE的度数是( )
如图,在△ABC中D,E分别是AB,AC的中点,点F,G在BC上,且BC=4BF=4CG,EF与DG相交于点O,若∠DFE=40°,∠DGE=80°,那么∠DOE的度数是( )
 如图,在△ABC中D,E分别是AB,AC的中点,点F,G在BC上,且BC=4BF=4CG,EF与DG相交于点O,若∠DFE=40°,∠DGE=80°,那么∠DOE的度数是( )
如图,在△ABC中D,E分别是AB,AC的中点,点F,G在BC上,且BC=4BF=4CG,EF与DG相交于点O,若∠DFE=40°,∠DGE=80°,那么∠DOE的度数是( )| A. | 100° | B. | 120° | C. | 140° | D. | 160° |
11.下列说法:
①一组对边平行,另一组对边相等的四边形是平行四边形;
②两条对角线相等且互相平分的四边形是矩形;
③在反比例函数y=$\frac{4}{x}$中,如果自变量x<2时,那么函数值y>2.
其中正确的有( )
①一组对边平行,另一组对边相等的四边形是平行四边形;
②两条对角线相等且互相平分的四边形是矩形;
③在反比例函数y=$\frac{4}{x}$中,如果自变量x<2时,那么函数值y>2.
其中正确的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
15.以长度分别为下列各组数的线段为边,其中能构成直角三角形的是( )
| A. | 1,2,3 | B. | 2,$\sqrt{2}$,$\sqrt{3}$ | C. | 6,8,10 | D. | 2,1.5,0.5 |
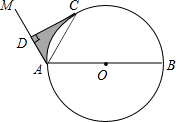 如图,AB是⊙O的直径,点C是⊙O上一点,连接AC,∠MAC=∠CAB,作CD⊥AM,垂足为D.
如图,AB是⊙O的直径,点C是⊙O上一点,连接AC,∠MAC=∠CAB,作CD⊥AM,垂足为D.