题目内容
1．
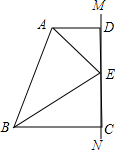如图，AD∥BC，∠ABC与∠BAD的平分线BE、AE相交于点E，过点E作直线MN⊥AD，交AD于点D，交BE于点C，试判断CE和DE的大小关系，并说明理由．
分析 CE=DE，如图，过点E作EF⊥AB于点F，利用角平分线的性质，得到ED=EF，EF=EC，所以可得DE=CE．
解答 解：CE=DE，
如图，过点E作EF⊥AB于点F，
∵MN⊥AD，
∴∠ADC=90°，
∵AD∥BC，
∴∠ADE+∠BCE=90°，
∴∠BCE=90°，
∵∠ABC与∠BAD的平分线BE、AE相交于点E，
∴ED=EF，EF=EC，
∴DE=CE．
点评 本题考查了角平分线的性质，解决本题的关键是作出辅助线，利用角平分线的性质得到相等的线段．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
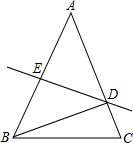如图，在△ABC中，AB=AC，∠A=36°，AB的垂直平分线DE交AC于D，交AB于E，若AC=7，BC=5，则BD+DE=$\frac{\sqrt{51}}{2}$+5．
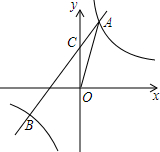如图，反比例函数y=$\frac{2}{x}$的图象与一次函数y=kx+b的图象交于点A（m，2），点B（-2，n ），一次函数图象与y轴的交点为C．