题目内容
11.计算已知a=($\frac{3}{2}$)2,b=-$\sqrt{2}$,c=-|-4|,d=1-(-$\sqrt{2}$),e=$\frac{22}{9}$,请你列式表示上述5个数中“无理数的和”与“有理数的积”的差,并计算结果.分析 首先分别找出无理数和有理数,然后求出无理数的和与有理数的积,最后求差.
解答 解:无理数为:b、d,
有理数为:a、c、e,
则b+d=1,ace=-22,
1-(-22)=23.
点评 本题考查了实数的运算,解答本题的关键是找出无理数和有理数,然后求出无理数的和与有理数的积.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
3.抛物线y=2x2+4x-1的顶点关于原点对称的点的坐标是( )
| A. | (-1,3) | B. | (-1,-3) | C. | (1,3) | D. | (1,-3) |
20.十一国庆期间,俄罗斯特技飞行队在黄山湖公园特技表演,其中一架飞机起飞后的高度变化如下表:请解答下列问题(写出计算过程)
(1)此时这架飞机比起飞点高了多少千米?
(2)如果飞机每上升或下降1千米需消耗2升燃油,那么这架飞机在这4个动作表演过程中,一共消耗了多少升燃油?
(3)如果飞机做特技表演时,有4个规定动作,起飞后高度变化如下:上升3.8千米,下降2.9千米,再上升1.6千米.若要使飞机最终比起飞点高出1千米,问第4个动作是上升还是下降,上升或下降多少千米?
| 高度变化 | 记作 |
| 上升4.4km | 4.4km |
| 下降3.2km | -3.2km |
| 上升1.1km | +1.1km |
| 下降1.5km | -1.5km |
(2)如果飞机每上升或下降1千米需消耗2升燃油,那么这架飞机在这4个动作表演过程中,一共消耗了多少升燃油?
(3)如果飞机做特技表演时,有4个规定动作,起飞后高度变化如下:上升3.8千米,下降2.9千米,再上升1.6千米.若要使飞机最终比起飞点高出1千米,问第4个动作是上升还是下降,上升或下降多少千米?
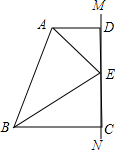 如图,AD∥BC,∠ABC与∠BAD的平分线BE、AE相交于点E,过点E作直线MN⊥AD,交AD于点D,交BE于点C,试判断CE和DE的大小关系,并说明理由.
如图,AD∥BC,∠ABC与∠BAD的平分线BE、AE相交于点E,过点E作直线MN⊥AD,交AD于点D,交BE于点C,试判断CE和DE的大小关系,并说明理由.