题目内容
2.已知x3+$\frac{1}{8}$=0,求代数式$\frac{3-x}{2x-4}$÷(x+2-$\frac{5}{x-2}$)的值.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,求出x的值,代入计算即可求出值.
解答 解:原式=-$\frac{x-3}{2(x-2)}$÷$\frac{(x+3)(x-3)}{x-2}$=-$\frac{x-3}{2(x-2)}$•$\frac{x-2}{(x+3)(x-3)}$=-$\frac{1}{2(x+3)}$,
由x3+$\frac{1}{8}$=0,得到x=-$\frac{1}{2}$,
则原式=-$\frac{1}{5}$.
点评 此题考查了分式的化简求值,以及立方根,熟练掌握通分及约分性质是解本题的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
10. 如图,△ABC中,若∠B=∠C,BD=CE,CD=BF,∠A=40°,则∠EDF=( )
如图,△ABC中,若∠B=∠C,BD=CE,CD=BF,∠A=40°,则∠EDF=( )
 如图,△ABC中,若∠B=∠C,BD=CE,CD=BF,∠A=40°,则∠EDF=( )
如图,△ABC中,若∠B=∠C,BD=CE,CD=BF,∠A=40°,则∠EDF=( )| A. | 80° | B. | 45° | C. | 60° | D. | 70° |
7.当温度不变时,气球内气体的气压P(单位:kPa)是气体体积V(单位:m3)的函数,下表记录了一组实验数据:P与V的函数关系式可能是( )
| V(单位:m3) | 1 | 1.5 | 2 | 2.5 | 3 |
| P(单位:kPa) | 96 | 64 | 48 | 38.4 | 32 |
| A. | P=96V | B. | P=-16V+112 | C. | P=16V2-96V+176 | D. | P=$\frac{96}{V}$ |
14. 如图,正方形ABCD的边长为2,其面积记作S1,以CD为斜边作等腰直角三角形,以该等腰三角形的一条直角边为边向外作正方形,其面积记作S2,…,按照此规律继续下去,则S2017的值为( )
如图,正方形ABCD的边长为2,其面积记作S1,以CD为斜边作等腰直角三角形,以该等腰三角形的一条直角边为边向外作正方形,其面积记作S2,…,按照此规律继续下去,则S2017的值为( )
 如图,正方形ABCD的边长为2,其面积记作S1,以CD为斜边作等腰直角三角形,以该等腰三角形的一条直角边为边向外作正方形,其面积记作S2,…,按照此规律继续下去,则S2017的值为( )
如图,正方形ABCD的边长为2,其面积记作S1,以CD为斜边作等腰直角三角形,以该等腰三角形的一条直角边为边向外作正方形,其面积记作S2,…,按照此规律继续下去,则S2017的值为( )| A. | ($\frac{\sqrt{2}}{2}$)2014 | B. | ($\frac{1}{2}$)2014 | C. | ($\frac{\sqrt{2}}{2}$)2015 | D. | ($\frac{1}{2}$)2015 |
12.下列运算正确的是( )
| A. | a3÷a2=1 | B. | (a2b)3=a2b3 | C. | (a2)5=a7 | D. | 3a•2a2=6a3 |
 如图,△ABC中,AC=13,AB=12,BC=5,CD是△ABC的角平分线,DE⊥AC于E,连结EB.
如图,△ABC中,AC=13,AB=12,BC=5,CD是△ABC的角平分线,DE⊥AC于E,连结EB.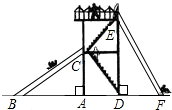 如图有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,若∠CBA=32°,求∠FED和∠EFD的度数.
如图有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,若∠CBA=32°,求∠FED和∠EFD的度数.