题目内容
5.二次函数y=kx2-6x+3的图象与x轴有交点,则k的取值范围是( )| A. | k≤3且k≠0 | B. | k<3且k≠0 | C. | k≤3 | D. | k<3 |
分析 根据二次函数的定义得到k≠0,根据△=b2-4ac决定抛物线与x轴的交点个数可得到△=(-6)2-4k•3≥0,然后求出两不等式的公共部分即可.
解答 解:∵二次函数y=kx2-6x+3的图象与x轴有交点,
∴k≠0且△=(-6)2-4k•3≥0,
∴k≤3且k≠0.
故选A.
点评 本题考查了抛物线与x轴的交点:对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
8.若函数y=(2m+1)x2+(1-2m)x+1(m为常数)是一次函数,则m的值为( )
| A. | m$>\frac{1}{2}$ | B. | m=$\frac{1}{2}$ | C. | m$<\frac{1}{2}$ | D. | m=-$\frac{1}{2}$ |
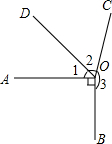 (1)从点O引四条射线OA,OB,OC,OD,如果∠AOB:∠BOC:∠COD:∠DOA=1:2:3:4,那么这四个角的度数分别是多少?
(1)从点O引四条射线OA,OB,OC,OD,如果∠AOB:∠BOC:∠COD:∠DOA=1:2:3:4,那么这四个角的度数分别是多少?
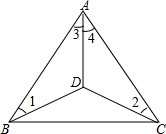 已知,如图△ABC中,BD=DC,∠1=∠2,求证:∠3=∠4.
已知,如图△ABC中,BD=DC,∠1=∠2,求证:∠3=∠4.