题目内容
6.(1)计算:(cos230°+sin230°)×tan60°(2)解方程:x2-2$\sqrt{3}$x-1=0.
分析 (1)利用特殊角的三角函数值得到原式=[($\frac{\sqrt{3}}{2}$)2+($\frac{1}{2}$)2]×$\sqrt{3}$,然后进行二次根式的混合计算;
(2)利用公式法解方程.
解答 解:(1)原式=[($\frac{\sqrt{3}}{2}$)2+($\frac{1}{2}$)2]×$\sqrt{3}$
=$\sqrt{3}$;
(2)△=(-2$\sqrt{3}$)2-4×(-1)
=16,
x=$\frac{2\sqrt{3}±4}{2}$=$\sqrt{3}$±2,
所以x1=$\sqrt{3}$+2,x2=$\sqrt{3}$-2.
点评 本题考查了解一元二次方程-公式法:用求根公式解一元二次方程的方法是公式法.

练习册系列答案
相关题目
4.下列方程,不适宜用因式分解法求解的是( )
| A. | x2=3x | B. | (x-2)2=3x-6 | C. | 4x2+4x+1=0 | D. | (x+2)(2x-1)=5 |
14.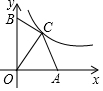 如图,在平面直角坐标系中,点A,B分别在x轴、y轴的正半轴上,OA=6,OB=9,点C在函数y=$\frac{k}{x}$(x>0)的图象上,当点C的横坐标为4时,△OAC与△OBC的面积相等,k的值为( )
如图,在平面直角坐标系中,点A,B分别在x轴、y轴的正半轴上,OA=6,OB=9,点C在函数y=$\frac{k}{x}$(x>0)的图象上,当点C的横坐标为4时,△OAC与△OBC的面积相等,k的值为( )
 如图,在平面直角坐标系中,点A,B分别在x轴、y轴的正半轴上,OA=6,OB=9,点C在函数y=$\frac{k}{x}$(x>0)的图象上,当点C的横坐标为4时,△OAC与△OBC的面积相等,k的值为( )
如图,在平面直角坐标系中,点A,B分别在x轴、y轴的正半轴上,OA=6,OB=9,点C在函数y=$\frac{k}{x}$(x>0)的图象上,当点C的横坐标为4时,△OAC与△OBC的面积相等,k的值为( )| A. | 16 | B. | 24 | C. | 30 | D. | 36 |
1.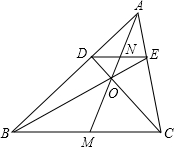 如图,△ABC中,DE∥BC,BE与CD交于点O,AO与DE、BC交于N、M,则下列式子中错误的是( )
如图,△ABC中,DE∥BC,BE与CD交于点O,AO与DE、BC交于N、M,则下列式子中错误的是( )
 如图,△ABC中,DE∥BC,BE与CD交于点O,AO与DE、BC交于N、M,则下列式子中错误的是( )
如图,△ABC中,DE∥BC,BE与CD交于点O,AO与DE、BC交于N、M,则下列式子中错误的是( )| A. | $\frac{DN}{BM}$=$\frac{AD}{AB}$ | B. | $\frac{AD}{AB}$=$\frac{DE}{BC}$ | C. | $\frac{DO}{OC}$=$\frac{DE}{BC}$ | D. | $\frac{AE}{EC}$=$\frac{AO}{OM}$ |
11.小派同学想给数学老师送张生日贺卡,但他只知道老师的生日在10月,那么他一次猜中老师生日的概率是( )
| A. | $\frac{1}{28}$ | B. | $\frac{1}{29}$ | C. | $\frac{1}{30}$ | D. | $\frac{1}{31}$ |
 如图,在四边形ABCD中,AB=CD,BC=AD,若∠A=130°,则∠C=130度.
如图,在四边形ABCD中,AB=CD,BC=AD,若∠A=130°,则∠C=130度.