题目内容
14.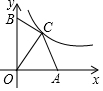 如图,在平面直角坐标系中,点A,B分别在x轴、y轴的正半轴上,OA=6,OB=9,点C在函数y=$\frac{k}{x}$(x>0)的图象上,当点C的横坐标为4时,△OAC与△OBC的面积相等,k的值为( )
如图,在平面直角坐标系中,点A,B分别在x轴、y轴的正半轴上,OA=6,OB=9,点C在函数y=$\frac{k}{x}$(x>0)的图象上,当点C的横坐标为4时,△OAC与△OBC的面积相等,k的值为( )| A. | 16 | B. | 24 | C. | 30 | D. | 36 |
分析 先设C(4,b),则k=4b,根据OAC与△OBC的面积相等,即可得到$\frac{1}{2}$×6×b=$\frac{1}{2}$×9×4,进而得到b=6,根据点C的坐标即可得到k的值.
解答 解:设C(4,b),则k=4b,
∵OAC与△OBC的面积相等,
∴$\frac{1}{2}$×6×b=$\frac{1}{2}$×9×4,
解得b=6,
∴k=4×6=24,
故选:B.
点评 本题主要考查了反比例函数图象上点的坐标特征,解决问题的关键是依据OAC与△OBC的面积相等列方程求解.

练习册系列答案
相关题目
 如图,四边形ABCD中,AD=CD,AB=BC,AC与BD交于点O.我们把这种两组邻边分别相等的四边形叫做“筝形”.请你猜想筝形的两条对角线AC与BD之间的位置关系,并证明你的结论.
如图,四边形ABCD中,AD=CD,AB=BC,AC与BD交于点O.我们把这种两组邻边分别相等的四边形叫做“筝形”.请你猜想筝形的两条对角线AC与BD之间的位置关系,并证明你的结论. 用5个完全相同的小正方体组成如图所示的立体图形,将右上角的小正方体拿掉后俯视图为( )
用5个完全相同的小正方体组成如图所示的立体图形,将右上角的小正方体拿掉后俯视图为( )



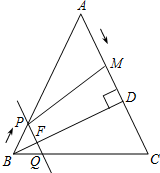 如图,在△ABC中,AB=AC=10cm,BD⊥AC于点D,且BD=8cm.点M从点A出发,沿AC的方向匀速运动,速度为2cm/秒;同时直线PQ由点B出发,沿BA的方向匀速运动,速度为1cm/秒,运动过程中始终保持PQ∥AC,直线PQ交AB于点P、交BC于点Q、交BD于点F.连接PM,设运动时间为t秒(0<t<5).
如图,在△ABC中,AB=AC=10cm,BD⊥AC于点D,且BD=8cm.点M从点A出发,沿AC的方向匀速运动,速度为2cm/秒;同时直线PQ由点B出发,沿BA的方向匀速运动,速度为1cm/秒,运动过程中始终保持PQ∥AC,直线PQ交AB于点P、交BC于点Q、交BD于点F.连接PM,设运动时间为t秒(0<t<5).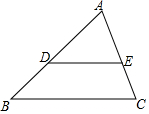 如图,在△ABC中,$\frac{AD}{DB}$=$\frac{AE}{EC}$,AB=12,AE=6,EC=4.则AD=$\frac{36}{5}$.
如图,在△ABC中,$\frac{AD}{DB}$=$\frac{AE}{EC}$,AB=12,AE=6,EC=4.则AD=$\frac{36}{5}$.