题目内容
10．已知直线y=2x+4与x轴交于点A，与y轴交于点B，点P在坐标轴上，且PO=240．求△ABP的面积．分析 先求出AB两点的坐标，由于P点的位置不能确定，故应分点P在x轴上、点P在y轴上两种情况进行讨论．
解答 解：∵直线y=2x+4与x轴交于点A，与y轴交于点B，
∴A（-2，0），B（0，4），
当点P在x轴的正半轴上时，S△ABP=S△AOB+S△OBP=$\frac{1}{2}$×2×4+$\frac{1}{2}$×4×240=484；
当点P在x轴的负半轴上时，S△ABP=S△OBP-S△AOB=$\frac{1}{2}$×4×240-$\frac{1}{2}$×2×4=476；
当点P在y轴的正半轴上时，S△ABP=S△OAP-S△AOB=$\frac{1}{2}$×2×240-$\frac{1}{2}$×2×4=236；
当点P在y轴的负半轴上时，S△ABP=S△OAP+S△AOB=$\frac{1}{2}$×2×240+$\frac{1}{2}$×2×4=244．
故△ABP的面积为484或476或236或244．
点评 本题考查的是一次函数图象上点的坐标特点，解答此题时要注意进行分类讨论，不要漏解．
练习册系列答案
相关题目
如图，在平面直角坐标系xOy中，菱形MNPQ的顶点P的坐标为（2，0），点N的坐标为（0，1），点M在第一象限，对角线NQ与x轴平行，直线y=x+8与x轴、y轴分别交于点A、B，将菱形MNPQ沿x轴向左平移k个单位，当点M落在△AOB内部时（不包括三角形的边），下列数据中不可能为k的值的是（ ）
如图，一次函数y=kx+b（k≠0）的图象过点P（-$\frac{3}{2}$，0）且与反比例函数y=$\frac{m}{x}$（m≠0）的图象相交于点A（2，1）和点B．
已知，在△ABC中，∠C=90°，点D是AB上一点，DE⊥BC，垂足是点E，且BE=AC，若BD=$\frac{1}{2}$，DE+BC=1．求证：∠ABC=30°．
如图，反比例函数y=$\frac{k}{x}$的图象与矩形AOBC的边AC交于E，且AE=2CE，与另一边BC交于点D，连接DE，若S△CED=1，则k的值为12．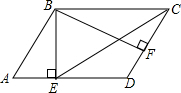
如图，在?ABCD中，BE⊥AD于E，BF⊥CD于F，若∠EBF=60°，AE=3，DF=2，则BE的长为3$\sqrt{3}$．