Question

19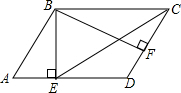．如图，在?ABCD中，BE⊥AD于E，BF⊥CD于F，若∠EBF=60°，AE=3，DF=2，则BE的长为3$\sqrt{3}$．

Answer 1

分析 由?ABCD中，BE⊥AD，BF⊥CD，可得∠D=120°，继而求得∠A的度数，然后由三角函数的性质求得答案．

解答 解：∵BE⊥AD，BF⊥CD，
∴∠BFD=∠BED=∠BEA=90°，
∵∠EBF=60°，
∴∠D=120°，
∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠BCD=∠A=60°，
∴BE=AE•tan60°=3×$\sqrt{3}$=3$\sqrt{3}$．
故答案为：3$\sqrt{3}$．

点评 此题考查了平行四边形的性质以及三角函数的知识．注意求得∠A的度数是解此题的关键．