题目内容
9. 如图,直线y=x+1分别与x轴、y轴相交于点A,B,以点A为圆心,AB长为半径画弧交x轴于点A1,再过点A1作x轴的垂线交直线于点B1,以点A为圆心,AB1长为半径画弧交x轴于点A2,…,按此做法进行下去,则点B4的坐标是( )
如图,直线y=x+1分别与x轴、y轴相交于点A,B,以点A为圆心,AB长为半径画弧交x轴于点A1,再过点A1作x轴的垂线交直线于点B1,以点A为圆心,AB1长为半径画弧交x轴于点A2,…,按此做法进行下去,则点B4的坐标是( )| A. | (2$\sqrt{2}$,2$\sqrt{2}$) | B. | (3,4) | C. | (4,4) | D. | (4$\sqrt{2}$-1,4$\sqrt{2}$) |
分析 根据题意,利用勾股定理求出AA1,AA2,AA3,AA4的长,得到各点坐标,找到规律即可解答.
解答 解:∵当x=0时,y=1;
当y=0时,x=-1;
∴A(-1,0),B(0,1),
AA1=AB=$\sqrt{{OA}^{2}+{OB}^{2}}$=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$;
AA2=AB1=$\sqrt{{(\sqrt{2})}^{2}+{(\sqrt{2})}^{2}}$=2,
AA3=AB2=$\sqrt{{2}^{2}+{2}^{2}}$=$\sqrt{8}$,
AA4=AB3=$\sqrt{{(\sqrt{8})}^{2}+{(\sqrt{8})}^{2}}$=4,
∴A4(3,0),
∴B4(3,4).
故选B.
点评 本题考查的是一次函数图象上点的坐标特点,解答此题的关键是根据勾股定理求出AA4的长,再得出A4的坐标,根据点B在直线y=x+1上得出结论.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
20.关于x、y的方程组$\left\{\begin{array}{l}{2x+3y=k}\\{3x+2y=k+2}\end{array}\right.$的解x、y的和为4,则k的值为( )
| A. | 16 | B. | 17 | C. | 9 | D. | 19 |
18.(-$\frac{1}{2}$)3的倒数是( )
| A. | -8 | B. | -$\frac{1}{8}$ | C. | 8 | D. | $\frac{1}{8}$ |
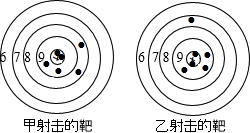 如图是甲乙两人在一次射击比赛中靶的情况(击中靶中心的圆面为10环,靶中数字表示该数所在圆环被击中所得的环数),每人射击了6次.
如图是甲乙两人在一次射击比赛中靶的情况(击中靶中心的圆面为10环,靶中数字表示该数所在圆环被击中所得的环数),每人射击了6次.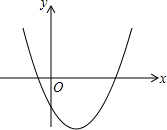 在二次函数y=ax2+bx+c的图象如图所示,下列说法中:①b2-4ac<0;②$-\frac{b}{2a}$>0;③abc>0;④a-b-c>0,说法正确的是②③④(填序号).
在二次函数y=ax2+bx+c的图象如图所示,下列说法中:①b2-4ac<0;②$-\frac{b}{2a}$>0;③abc>0;④a-b-c>0,说法正确的是②③④(填序号).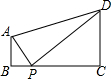 如图,AB⊥BC,DC⊥BC,AB=1,DC=2,BC=3,点P是线段BC上一动点(不与点B、C重合),若△APD是等腰三角形,则CP的长是1或$\sqrt{6}$.
如图,AB⊥BC,DC⊥BC,AB=1,DC=2,BC=3,点P是线段BC上一动点(不与点B、C重合),若△APD是等腰三角形,则CP的长是1或$\sqrt{6}$. 如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE,F为AB中点,连接DF、EF,DE、EF与AC交于点O,DE与AB交于点G,连接OG,若∠BAC=30°,下列结论:
如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE,F为AB中点,连接DF、EF,DE、EF与AC交于点O,DE与AB交于点G,连接OG,若∠BAC=30°,下列结论: 如图,将三角形ABC纸片沿MN折叠,使点A落在点A′处,若∠A′MB=55°,则∠AMN=62.5°.
如图,将三角形ABC纸片沿MN折叠,使点A落在点A′处,若∠A′MB=55°,则∠AMN=62.5°.