题目内容
20．关于x、y的方程组$\left\{\begin{array}{l}{2x+3y=k}\\{3x+2y=k+2}\end{array}\right.$的解x、y的和为4，则k的值为（ ）| A． | 16 | B． | 17 | C． | 9 | D． | 19 |
分析 方程组两方程相加表示出x+y，代入x+y=4求出k的值即可．
解答 解：$\left\{\begin{array}{l}{2x+3y=k①}\\{3x+2y=k+2②}\end{array}\right.$，
①+②得：5（x+y）=2k+2，即x+y=$\frac{2k+2}{5}$，
根据题意得：$\frac{2k+2}{5}$=4，
解得：k=9．
故选C．
点评 此题考查了二元一次方程组的解，正确求出关于x，y的方程组的解是解本题的关键．
练习册系列答案
相关题目
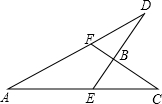如图，已知∠CBE=96°，∠A=27°，∠C=30°，则∠ADE=27°．
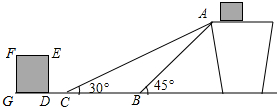如图，是某货运站传送货物的平面示意图．传送带AB长为4米，在离B点5米远的地方有一堆货物DEFG等待运输．为了提高传送过程的安全性，工人师傅欲减小传送带与地面的夹角，使其由45°改为30°．但要保证货物着地点C的左侧留出2米的通道，试判断货物DEFG是否需要挪走．（结果精确到0.1米：参考数据：$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73，$\sqrt{5}$≈2.24，$\sqrt{6}$≈2.45）
15．
有一种足球是由32块黑白相间的牛皮缝制而成的，黑皮可看作正五边形，白皮可看作正六边形（正多边形为各边相等，各内角相等的几何图形），那么白皮、黑皮的块数为（ ）
有一种足球是由32块黑白相间的牛皮缝制而成的，黑皮可看作正五边形，白皮可看作正六边形（正多边形为各边相等，各内角相等的几何图形），那么白皮、黑皮的块数为（ ）| A． | 18、14 | B． | 16、16 | C． | 20、12 | D． | 22、10 |
5．在5次数学单元测试中，甲、乙、丙、丁四名同学成绩的平均分均为88.5分，方差分别为S甲2=0.51，S乙2=0.41，S丙2=0.62，S丁2=0.45，则这四名同学中成绩最稳定的是（ ）
| A． | 甲 | B． | 乙 | C． | 丙 | D． | 丁 |
9．
如图，直线y=x+1分别与x轴、y轴相交于点A，B，以点A为圆心，AB长为半径画弧交x轴于点A1，再过点A1作x轴的垂线交直线于点B1，以点A为圆心，AB1长为半径画弧交x轴于点A2，…，按此做法进行下去，则点B4的坐标是（ ）
如图，直线y=x+1分别与x轴、y轴相交于点A，B，以点A为圆心，AB长为半径画弧交x轴于点A1，再过点A1作x轴的垂线交直线于点B1，以点A为圆心，AB1长为半径画弧交x轴于点A2，…，按此做法进行下去，则点B4的坐标是（ ）| A． | （2$\sqrt{2}$，2$\sqrt{2}$） | B． | （3，4） | C． | （4，4） | D． | （4$\sqrt{2}$-1，4$\sqrt{2}$） |
