题目内容
1.当a=$\sqrt{2}$+1,b=$\sqrt{3}$-1时,求代数式a2-b2的值.分析 直接把a、b的数值代入代数式求得答案即可.
解答 解:当a=$\sqrt{2}$+1,b=$\sqrt{3}$-1时,
原式=($\sqrt{2}$+1)2-($\sqrt{3}$-1)2
=3+2$\sqrt{2}$-4+2$\sqrt{3}$
=2$\sqrt{2}$+2$\sqrt{3}$-1.
点评 此题考查二次根式的化简求值,掌握完全平方公式和结果的化简是解决问题的关键.

练习册系列答案
相关题目
11.下列计算中,正确的是( )
| A. | 2a+3b=5ab | B. | (3a3)2=6a6 | C. | a6+a2=a3 | D. | -3a+2a=-a |
9.∠1和∠2是对顶角的图形为( )
| A. |  | B. |  | C. |  | D. |  |
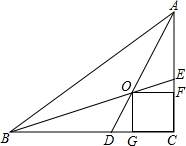 如图,在Rt△ABC中,两锐角的平分线AD,BE相交于点O,OF⊥AC于点F,OG⊥BC于点G,求证:四边形OGCF是正方形.
如图,在Rt△ABC中,两锐角的平分线AD,BE相交于点O,OF⊥AC于点F,OG⊥BC于点G,求证:四边形OGCF是正方形.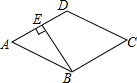 如图,在菱形ABCD中,∠ABC=120°,作BE⊥AD,垂足为点E,求证:AE=DE.
如图,在菱形ABCD中,∠ABC=120°,作BE⊥AD,垂足为点E,求证:AE=DE.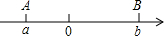 阅读下面材料:点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.回答下列问题:
阅读下面材料:点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a-b|.回答下列问题: