题目内容
6.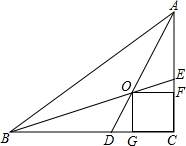 如图,在Rt△ABC中,两锐角的平分线AD,BE相交于点O,OF⊥AC于点F,OG⊥BC于点G,求证:四边形OGCF是正方形.
如图,在Rt△ABC中,两锐角的平分线AD,BE相交于点O,OF⊥AC于点F,OG⊥BC于点G,求证:四边形OGCF是正方形.
分析 根据有三个角是直角的四边形是矩形,可得四边形OGCF是矩形,根据角平分线的性质,可得OH与OF,OH与OG的关系,根据邻边相等的矩形是正方形,可得答案.
解答 证明:如图,作OH⊥AB与H点 ,
,
∵OF⊥AC于点F,OG⊥BC于点G,
∴∠OGC=∠OFC=90°.
∵∠C=90°,
∴四边形OGCF是矩形.
∵AD平分∠BAC,
∴OH=OF.
∵BE平分∠ABC,
∴OH=OG,
∴OF=OG,
∴四边形OGCF是正方形.
点评 本题考查了正方形的判定,利用了矩形的判定,正方形的判定,利用角平分线的性质得出邻边相等是解题关键.

练习册系列答案
相关题目
16.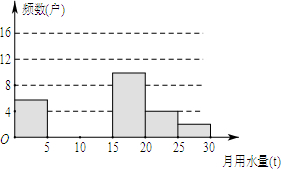 某校社会活动实践小组的同学们为了解2015年教工小区家庭月平均用水情况,随机调查了该小区部分家庭,并将调查数据整理成如下的统计表和直方图
某校社会活动实践小组的同学们为了解2015年教工小区家庭月平均用水情况,随机调查了该小区部分家庭,并将调查数据整理成如下的统计表和直方图
根据上述的数据整理信息,请解答以下问题:
(1)求出统计表中m,n的值;
(2)把频数分布直方图补充完整;
(3)若该小区有1500户家庭,根据调查数据估计,该小区月平均用水量超过20t的家庭大约有多少户?
 某校社会活动实践小组的同学们为了解2015年教工小区家庭月平均用水情况,随机调查了该小区部分家庭,并将调查数据整理成如下的统计表和直方图
某校社会活动实践小组的同学们为了解2015年教工小区家庭月平均用水情况,随机调查了该小区部分家庭,并将调查数据整理成如下的统计表和直方图| 月平均用水量x(t) | 频数(户) | 频率 |
| 0<x≤5 | 6 | 0.12 |
| 5<x≤10 | m | 0.24 |
| 10<x≤15 | n | 0.32 |
| 15<x≤20 | 10 | 0.20 |
| 20<x≤25 | 4 | k |
| 25<x≤30 | 2 | 0.04 |
(1)求出统计表中m,n的值;
(2)把频数分布直方图补充完整;
(3)若该小区有1500户家庭,根据调查数据估计,该小区月平均用水量超过20t的家庭大约有多少户?

 如图,由两个等宽的矩形叠合而得到的四边形ABCD是菱形吗?证明你的结论.
如图,由两个等宽的矩形叠合而得到的四边形ABCD是菱形吗?证明你的结论.
 如图,若D是AB中点,AB=4,则DB=2.
如图,若D是AB中点,AB=4,则DB=2.