题目内容
9.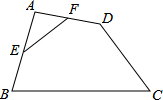 如图,在四边形ABCD中,E,F分别是AB,AD的中点.若EF=2,BC=5,CD=3,则sinC等于( )
如图,在四边形ABCD中,E,F分别是AB,AD的中点.若EF=2,BC=5,CD=3,则sinC等于( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
分析 如图,连接BD,由三角形中位线定理得到BD的长度,然后利用勾股定理的逆定理推知△BCD为直角三角形,最后由锐角三角函数的定义进行解答.
解答 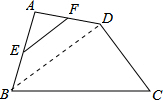 解:连接BD,
解:连接BD,
∵E、F分别是AB、AD的中点,
∴EF∥BD,EF=$\frac{1}{2}$BD,
∵EF=2,
∴BD=4,
又∵BC=5,CD=3,
∴BD2+CD2=BC2,
∴△BDC是直角三角形,
∴sinC=$\frac{BD}{BC}$=$\frac{4}{5}$,
故选:C.
点评 此题主要考查了锐角三角形的定义以及三角形中位线的性质以及勾股定理逆定理,根据已知得出△BDC是直角三角形是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.为缓解甲、乙两地旱情,某水库计划向甲、乙两地送水,甲地需水量为180万立方米,乙地需电水量为120万立方米,现已两次送水:往甲地送水3天,乙地送水2天,共送水84万立方米;往甲地送水2天,乙地送水3天,共送水81万立方米,则完成往甲地,乙地送水任务还各需( )天.
| A. | 甲需4天,乙需2天 | B. | 甲需3天,乙需1天 | C. | 甲需6天,乙需4天 | D. | 甲需5天,乙需3天 |
17.一元二次方程x(x-2)+x-2=0的解是( )
| A. | x1=2,x2=-1 | B. | x1=1,x2=-2 | C. | x1=3,x2=-2 | D. | x1=2,x2=-3 |
 已知:如图,反比例函数y=$\frac{k}{x}$(k≠0)与一次函数y=ax+b(a≠0)的图象交于A(3,1)、B(m,-3)两点.
已知:如图,反比例函数y=$\frac{k}{x}$(k≠0)与一次函数y=ax+b(a≠0)的图象交于A(3,1)、B(m,-3)两点. 在长为30,宽为20的矩形纸片上,如图所示剪去四个边长为x的小正方形,若剪去部分的面积等于剩余部分的面积.
在长为30,宽为20的矩形纸片上,如图所示剪去四个边长为x的小正方形,若剪去部分的面积等于剩余部分的面积.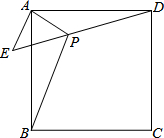 如图,已知ABCD为正方形,△AEP为等腰直角三角形,∠EAP=90°,EA=AP=1,且D、P、E三点共线,若PB=$\sqrt{5}$,则PC=$\sqrt{3}$.
如图,已知ABCD为正方形,△AEP为等腰直角三角形,∠EAP=90°,EA=AP=1,且D、P、E三点共线,若PB=$\sqrt{5}$,则PC=$\sqrt{3}$.