题目内容
17.为了推动学校读书活动的开展,吴扬对所在班一周读书情况做了调查,调查结果统计如图(其中男生一周读书3次的人数没有标出)所示,根据上述信息,解答下列各题:(1)该班女生人数是20;
(2)试说明女生一周读书次数的中位数和男生一周读书次数的平均数相同;
(3)如果学校规定,一周读书不低于3次的同学为“合格”,如果该班女生“合格”人数不超过男生“合格”人数的65%,请求该班男生每周读书次数为3的最少人数.
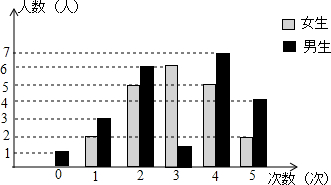
分析 (1)根据统计图中的数据可以求得女生的人数;
(2)根据统计图中的数据可以分别求得女生一周读书次数的中位数和男生一周读书次数的平均数,从而可以解答本题;
(3)根据题意和统计图中的数据可以求得该班男生每周读书次数为3的最少人数.
解答 解:(1)由图可得,
该班女生人数为:2+5+6+5+2=20,
故答案为:20;
(2)由题意和统计图中的数据可知,
女生一周读书次数的中位数是3,
设男生一周读书3次的人数为x人,
则男生一周读书次数的平均数是:$\frac{0×1+1×3+2×6+3x+4×7+5×4}{1+3+6+x+7+4}$=$\frac{0+3+12+3x+28+20}{21+x}$=$\frac{63+3x}{21+x}$=3,
故女生一周读书次数的中位数和男生一周读书次数的平均数相同;
(3)由题意可得,
6+5+2≤(x+7+4)×65%,
解得,x≥9,
∴该班男生每周读书次数为3的最少为3人.
点评 本题考查条形统计图、算术平均数、中位数,解答本题的关键是明确题意,找出所求问题需要的条件,利用条形统计图解答问题.

练习册系列答案
相关题目
 已知,如图,∠1=∠2,∠B=∠C.
已知,如图,∠1=∠2,∠B=∠C.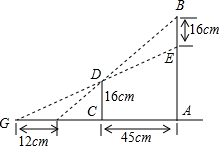 如图,明珠大厦的顶部建有一直径为16m的“明珠”,它的西面45m处有一高16m的小型建筑CD,人站在CD的西面附近无法看到“明珠”的外貌,如果向西走到点F处,可以开始看到“明珠”的顶端B;若想看到“明珠”的全貌,必须往西至少再走12m,求大厦主体建筑的高度AE(不含顶部的“明珠”部分的高度)
如图,明珠大厦的顶部建有一直径为16m的“明珠”,它的西面45m处有一高16m的小型建筑CD,人站在CD的西面附近无法看到“明珠”的外貌,如果向西走到点F处,可以开始看到“明珠”的顶端B;若想看到“明珠”的全貌,必须往西至少再走12m,求大厦主体建筑的高度AE(不含顶部的“明珠”部分的高度)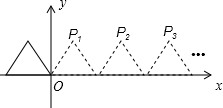 如图,将边长为2的等边三角形沿x轴正方形连续翻折2014次,依次得到点P1、P2、P3、…、P2014,则点P2014的坐标是(4027,$\sqrt{3}$).
如图,将边长为2的等边三角形沿x轴正方形连续翻折2014次,依次得到点P1、P2、P3、…、P2014,则点P2014的坐标是(4027,$\sqrt{3}$). “十一黄金周”期间,小明一家自驾游去了离家170千米的某地,下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.
“十一黄金周”期间,小明一家自驾游去了离家170千米的某地,下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象.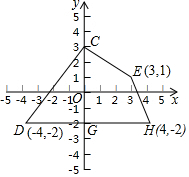 在平面直角坐标系中,四边形CDHE的位置如图所示,求四边形CDHE的面积.
在平面直角坐标系中,四边形CDHE的位置如图所示,求四边形CDHE的面积.