题目内容
7.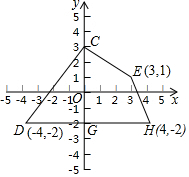 在平面直角坐标系中,四边形CDHE的位置如图所示,求四边形CDHE的面积.
在平面直角坐标系中,四边形CDHE的位置如图所示,求四边形CDHE的面积.
分析 过点E作EF⊥DH于F,然后根据四边形CDHE的面积等于两个直角三角形的面积与一个梯形的面积的和列式计算即可得解.
解答  解:如图,过点E作EF⊥DH于F,
解:如图,过点E作EF⊥DH于F,
四边形CDHE的面积=S△CDG+S梯形CGFE+S△EFH,
=$\frac{1}{2}$×4×5+$\frac{1}{2}$×(3+5)×3+$\frac{1}{2}$×1×3,
=10+12+1.5,
=23.5.
点评 本题考查了坐标与图形性质,主要是不规则四边形的面积的求解,作辅助线将不规则四边形分割成规则的三角形与梯形是解题的关键.

练习册系列答案
相关题目
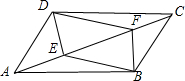 已知:如图,四边形ABCD为平行四边形,E,F是对角线AC上的两点,AE=CF,连接DE,BE,BF,求证:四边形DEBF是平行四边形.
已知:如图,四边形ABCD为平行四边形,E,F是对角线AC上的两点,AE=CF,连接DE,BE,BF,求证:四边形DEBF是平行四边形.