��Ŀ����
4�� ���壺����ƽ��ֱ������ϵxOy�е��߶�PQ�͵�M���ڡ�MPQ�У���PQ���ϵĸ�Ϊ2ʱ����MΪPQ�ġ��ȸߵ㡱���ƴ�ʱMP+MQΪPQ�ġ��ȸ߾��롱��
���壺����ƽ��ֱ������ϵxOy�е��߶�PQ�͵�M���ڡ�MPQ�У���PQ���ϵĸ�Ϊ2ʱ����MΪPQ�ġ��ȸߵ㡱���ƴ�ʱMP+MQΪPQ�ġ��ȸ߾��롱����1����P��1��2����Q��4��2����
���ڵ�A��1��0����B��$\frac{5}{2}$��4����C��0��3���У�PQ�ġ��ȸߵ㡱��A��B��
����M��t��0��ΪPQ�ġ��ȸߵ㡱����PQ�ġ��ȸ߾��롱����Сֵ����ʱt��ֵ��
��2����P��0��0����PQ=2����PQ�ġ��ȸߵ㡱��y�����������ҡ��ȸ߾��롱��Сʱ��ֱ��д����Q�����꣮
���� ��1�����ݡ��ȸߵ㡱�ĸ����ɣ�
��2������ȷ������P����x��ĶԳƵ�P�䣬�ٸ������·��������ȷ����С���룻����֤�����ȸ߾��롱��Сʱ��MPQΪ���������Σ������ù��ɶ��������Q���꼴�ɣ�
��� �⣺��1���١�P��1��2����Q��4��2����
���ڵ�A��1��0����B��$\frac{5}{2}$��4����PQ�ľ���Ϊ2��
��PQ�ġ��ȸߵ㡱��A��B��
�ʴ�Ϊ��A��B��
����ͼ1������P����x��ĶԳƵ�P�䣬����P��Q��P��Q��x��Ľ��㼴Ϊ���ȸߵ㡱M����ʱ���ȸ߾��롱��С����СֵΪ�߶�P��Q�ij���
��P ��1��2����
��P�䣨1��-2����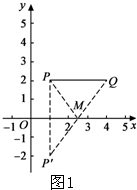
��ֱ��P��Q�ı���ʽΪy=kx+b��
�������⣬��$\left\{\begin{array}{l}{k+b=-2}\\{4k+b=2}\end{array}\right.$�����$\left\{\begin{array}{l}{k=\frac{4}{3}}\\{b=-\frac{10}{3}}\end{array}\right.$��
��ֱ��P��Q�ı���ʽΪ$y=\frac{4}{3}x-\frac{10}{3}$��
��y=0ʱ�����$x=\frac{5}{2}$��
��$t=\frac{5}{2}$��
�������⣬��֪PP��=4��PQ=3��PQ��PP�䣬
��$P'Q=\sqrt{PP{'^2}+P{Q^2}}=5$��
�ࡰ�ȸ߾��롱��СֵΪ5��
��2����ͼ2����PQ�ġ��ȸߵ㡱M��MN��PQ�ڵ�N��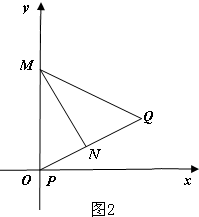
��PQ=2��MN=2��
��PN=x����NQ=2-x��
��Rt��MNP��Rt��MNQ���ɹ��ɶ����ã�
MP2=22+x2=4+x2��MQ2=22+��2-x��2=x2-4x+8��
��MP2+MQ2=2x2-4x+12=2��x-1��2+10��
��MP2+MQ2�ܣ�MP+MQ��2��
�൱MP2+MQ2��СʱMP+MQҲ��С����ʱx=1��
��PN=NQ��
���MPQ����������
��MP=MQ=$\sqrt{{2}^{2}+{1}^{2}}=\sqrt{5}$��
��ͼ3����Q����Ϊ��x��y��������Q��QE��y���ڵ�E��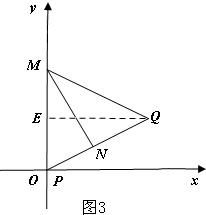
����Rt��MNP��Rt��MNQ���ɹ��ɶ����ã�
QE2=QP2-OE2=22-y2=4-y2��$Q{E}^{2}=Q{M}^{2}-M{E}^{2}=��\sqrt{5}��^{2}-��\sqrt{5}-y��^{2}$=$2\sqrt{5}y-{y}^{2}$��
��4-${y}^{2}=2\sqrt{5}y-{y}^{2}$��
���y=$\frac{2\sqrt{5}}{5}$��
$Q{E}^{2}=4-{y}^{2}=4-��\frac{2\sqrt{5}}{5}��^{2}=\frac{16}{5}$��
����Q�ڵ�һ����ʱx=$\frac{4\sqrt{5}}{5}$������Q�ڵڶ�����ʱx=-$\frac{4\sqrt{5}}{5}$��
��Q��$\frac{{4\sqrt{5}}}{5}$��$\frac{{2\sqrt{5}}}{5}$����Q��$-\frac{{4\sqrt{5}}}{5}$��$\frac{{2\sqrt{5}}}{5}$����
���� ���⿼���˶Զ����¸������������·�����⣬ȷ����P����x��ĶԳƵ�P���λ���ǽ������Ĺؼ���

| A�� | $\frac{900}{m}=\frac{750}{m+3}$ | B�� | $\frac{900}{m+3}=\frac{750}{m}$ | C�� | $\frac{900}{m}=\frac{750}{m-3}$ | D�� | $\frac{900}{m-3}=\frac{750}{m}$ |
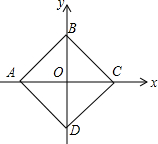 ��������ABCD�ĶԽ���AC��BD����ֱ��Ϊ�����ᣬ����ƽ��ֱ������ϵ����ͼ��ʾ����֪��A�������ǣ�-$\sqrt{2}$��0�����ֽ�������ABCD��ԭ��O˳ʱ����ת45�㣬����ת���C�Ķ�Ӧ�������ǣ�������
��������ABCD�ĶԽ���AC��BD����ֱ��Ϊ�����ᣬ����ƽ��ֱ������ϵ����ͼ��ʾ����֪��A�������ǣ�-$\sqrt{2}$��0�����ֽ�������ABCD��ԭ��O˳ʱ����ת45�㣬����ת���C�Ķ�Ӧ�������ǣ�������| A�� | ��$\sqrt{2}$��$\sqrt{2}$�� | B�� | ��$\sqrt{2}$��-$\sqrt{2}$�� | C�� | ��-1��1�� | D�� | ��1��-1�� |
| A�� | y1��y2��y3 | B�� | y2��y1��y3 | C�� | y3��y1��y2 | D�� | y3��y2��y1 |
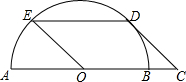 ��ͼ����C�ǰ�ԲO��ֱ��AB���ӳ�����һ�㣮CD���ԲO���У�DΪ�е㣬����D��DE��AB����ԲO�ڵ�E�����ı���OCDE��ƽ���ı��Σ�CD=4����ED�ij�Ϊ��������
��ͼ����C�ǰ�ԲO��ֱ��AB���ӳ�����һ�㣮CD���ԲO���У�DΪ�е㣬����D��DE��AB����ԲO�ڵ�E�����ı���OCDE��ƽ���ı��Σ�CD=4����ED�ij�Ϊ��������| A�� | 4 | B�� | 4$\sqrt{2}$ | C�� | 2$\sqrt{6}$ | D�� | 3$\sqrt{3}$ |
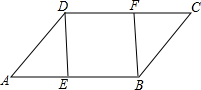 ��֪����ͼ����E��F�ֱ���?ABCD��AB��DC���ϵĵ㣬��AE=CF������DE��EF����֤���ı���DEBF��ƽ���ı��Σ�
��֪����ͼ����E��F�ֱ���?ABCD��AB��DC���ϵĵ㣬��AE=CF������DE��EF����֤���ı���DEBF��ƽ���ı��Σ�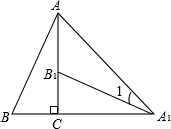 ��ͼ����Rt��ABC��ֱ�Ƕ���C˳ʱ����ת90�㣬�õ���A1B1C������AA1������AA1B1=15�㣬���B�Ķ�����60�㣮
��ͼ����Rt��ABC��ֱ�Ƕ���C˳ʱ����ת90�㣬�õ���A1B1C������AA1������AA1B1=15�㣬���B�Ķ�����60�㣮