题目内容
19.若(x+2)(x-3)>0,则x的取值范围是x>3或x<-2.分析 把原式化为两个一元一次不等式组,解不等式组得到答案.
解答 解:原式可化为①$\left\{\begin{array}{l}{x+2>0}\\{x-3>0}\end{array}\right.$和②$\left\{\begin{array}{l}{x+2<0}\\{x-3<0}\end{array}\right.$,
解①得x>3,
解②得x<-2.
故答案为:x>3或x<-2.
点评 本题考查的是一元一次不等式组的解法,根据乘法法则把原式化为两个一元一次不等式组是解题的关键.

练习册系列答案
相关题目
10.甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮15min到达点A,乙客轮用20min到达B点,若A、B两点的直线距离为1000m.甲客轮沿北偏东30°的方向航行,则乙客轮的航行方向可能是( )
| A. | 南偏东60° | B. | 南偏西30° | C. | 北偏西30° | D. | 南偏西60° |
9.某商场新进一批商品,每个成本价25元,销售一段时间发现销售量y(个)与销售单价x(元/个)之间成一次函数关系.
(1)根据表中提供的数据,求y与x之间的函数关系式;
(2)若该商品的销售单价在45元~80元之间浮动.
①销售单价定为多少元时,销售利润最大?此时销售量为多少?
②商店想要在这段时间内获得4550元的销售利润,销售单价应定为多少元?
| x(元/个) | 30 | 40 | 50 |
| y(个) | 190 | 170 | 150 |
(2)若该商品的销售单价在45元~80元之间浮动.
①销售单价定为多少元时,销售利润最大?此时销售量为多少?
②商店想要在这段时间内获得4550元的销售利润,销售单价应定为多少元?
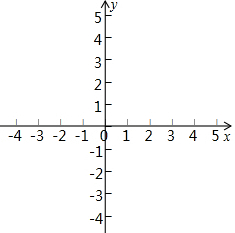 定义:对于平面直角坐标系xOy中的线段PQ和点M,在△MPQ中,当PQ边上的高为2时,称M为PQ的“等高点”,称此时MP+MQ为PQ的“等高距离”.
定义:对于平面直角坐标系xOy中的线段PQ和点M,在△MPQ中,当PQ边上的高为2时,称M为PQ的“等高点”,称此时MP+MQ为PQ的“等高距离”.