题目内容
12.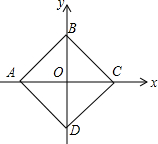 以正方形ABCD的对角线AC、BD所在直线为坐标轴,建立平面直角坐标系,如图所示,已知点A的坐标是(-$\sqrt{2}$,0),现将正方形ABCD绕原点O顺时针旋转45°,则旋转后点C的对应点坐标是( )
以正方形ABCD的对角线AC、BD所在直线为坐标轴,建立平面直角坐标系,如图所示,已知点A的坐标是(-$\sqrt{2}$,0),现将正方形ABCD绕原点O顺时针旋转45°,则旋转后点C的对应点坐标是( )| A. | ($\sqrt{2}$,$\sqrt{2}$) | B. | ($\sqrt{2}$,-$\sqrt{2}$) | C. | (-1,1) | D. | (1,-1) |
分析 利用旋转的性质结合正方形的性质得出EO=FO=1,进而得出旋转后点C的对应点坐标.
解答  解:如图所示:将正方形ABCD绕原点O顺时针旋转45°,得到如图所示图形,
解:如图所示:将正方形ABCD绕原点O顺时针旋转45°,得到如图所示图形,
∵点A的坐标是(-$\sqrt{2}$,0),
∴AO=CO=$\sqrt{2}$,
则OC′=$\sqrt{2}$,EO=FO,
故EO=FO=1,
则旋转后点C的对应点坐标是:(1,-1).
故选:D.
点评 此题主要考查了坐标与图形的性质以及正方形的性质,得出EO=FO的长是解题关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
1.某种商品的进价为40元/件,以获利不低于25%的价格销售时,商品的销售单价y(元/件)与销售数量x(件)(x是正整数)之间的关系如下表:
(1)由题意知商品的最低销售单价是50元,当销售单价不低于最低销售单价时,y是x的一次函数.求出y与x的函数关系式及x的取值范围;
(2)在(1)的条件下,当销售单价为多少元时,所获销售利润最大,最大利润是多少元?
| x(件) | … | 5 | 10 | 15 | 20 | … |
| y(元/件) | … | 75 | 70 | 65 | 60 | … |
(2)在(1)的条件下,当销售单价为多少元时,所获销售利润最大,最大利润是多少元?
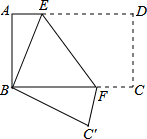 如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )
如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( ) 定义:对于平面直角坐标系xOy中的线段PQ和点M,在△MPQ中,当PQ边上的高为2时,称M为PQ的“等高点”,称此时MP+MQ为PQ的“等高距离”.
定义:对于平面直角坐标系xOy中的线段PQ和点M,在△MPQ中,当PQ边上的高为2时,称M为PQ的“等高点”,称此时MP+MQ为PQ的“等高距离”.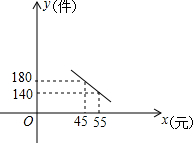 大学生王强积极响应“自主创业”的好种,准备投资销售一种进价为每件4元的小家电,通过试营销发现,当销售单价在40元至60元之间(含40元和60元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数,其图象如图所示.
大学生王强积极响应“自主创业”的好种,准备投资销售一种进价为每件4元的小家电,通过试营销发现,当销售单价在40元至60元之间(含40元和60元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数,其图象如图所示.