题目内容
14.若反比例函数y=$\frac{k}{x}$的图象经过点M(-3,4),则该图象必经过点( )| A. | P(3,-4) | B. | P(3,4) | C. | P(2,6) | D. | P(-2,-6) |
分析 把M点坐标代入反比例函数解析式可求得k的值,则可求得反比例函数解析式,再把选项中的点的坐标代入解析式进行判断即可.
解答 解:
∵反比例函数y=$\frac{k}{x}$的图象经过点M(-3,4),
∴k=-3×4=-12,
∴反比例函数解析式为y=$\frac{-12}{x}$,
当x=3时,y=$\frac{-12}{3}$=-4,故点(3,-4)在函数图象上,点(3,4)不在函数图象上,
当x=2时,y=$\frac{-12}{2}$=-6,故点(2,6)和点(-2,-6)不在函数图象上,
故选A.
点评 本题主要考查反比例函数图象上点的坐标特征,掌握函数图象上的点的坐标满足函数解析式是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.在下列实数:$\frac{π}{2}$、$\sqrt{3}$、$\root{3}{27}$、$\sqrt{16}$、$\frac{22}{7}$、-0.0010001中,有理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.下列运算正确的是( )
| A. | 2x2+x2=3x4 | B. | (-mn2)•(2mn)=-2m2n3 | C. | y8÷y2=y4 | D. | (3a2b)2=6a4b2 |
9. 如图,在点M,N,P,Q中,一次函数y=kx+2(k<0)的图象不可能经过的点是( )
如图,在点M,N,P,Q中,一次函数y=kx+2(k<0)的图象不可能经过的点是( )
 如图,在点M,N,P,Q中,一次函数y=kx+2(k<0)的图象不可能经过的点是( )
如图,在点M,N,P,Q中,一次函数y=kx+2(k<0)的图象不可能经过的点是( )| A. | M | B. | N | C. | P | D. | Q |
19. 如图,直线l与直线a,b相交,且a∥b,∠1=110°,则∠2的度数是( )
如图,直线l与直线a,b相交,且a∥b,∠1=110°,则∠2的度数是( )
 如图,直线l与直线a,b相交,且a∥b,∠1=110°,则∠2的度数是( )
如图,直线l与直线a,b相交,且a∥b,∠1=110°,则∠2的度数是( )| A. | 20° | B. | 70° | C. | 90° | D. | 110° |
6.在同一平面内,a、b、c是直线,下列说法正确的是( )
| A. | 若a∥b,b∥c 则 a∥c | B. | 若a⊥b,b⊥c,则a⊥c | ||
| C. | 若a∥b,b⊥c,则a∥c | D. | 若a∥b,b∥c,则a⊥c |
4.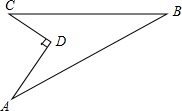 如图所示,有一块地ABCD,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,则这块地的面积为( )
如图所示,有一块地ABCD,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,则这块地的面积为( )
 如图所示,有一块地ABCD,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,则这块地的面积为( )
如图所示,有一块地ABCD,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,则这块地的面积为( )| A. | 60米2 | B. | 48米2 | C. | 30米2 | D. | 24米2 |