题目内容
4.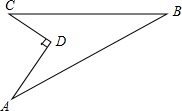 如图所示,有一块地ABCD,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,则这块地的面积为( )
如图所示,有一块地ABCD,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,则这块地的面积为( )| A. | 60米2 | B. | 48米2 | C. | 30米2 | D. | 24米2 |
分析 连接AC,利用勾股定理可以得出三角形ACD和ABC是直角三角形,△ABC的面积减去△ACD的面积就是所求的面积.
解答  解:连接AC,
解:连接AC,
∵∠ADC=90°,AD=4,CD=3,
∴AC2=AD2+CD2=42+32=25,
又∵AC>0,
∴AC=5,
又∵BC=12,AB=13,
∴AC2+BC2=52+122=169,
又∵AB2=169,
∴AC2+BC2=AB2,
∴∠ACB=90°,
∴S四边形ABCD=S△ABC-S△ADC=30-6=24米2.
故选D.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
14.若反比例函数y=$\frac{k}{x}$的图象经过点M(-3,4),则该图象必经过点( )
| A. | P(3,-4) | B. | P(3,4) | C. | P(2,6) | D. | P(-2,-6) |
15.已知圆锥的侧面展开图是一个半圆,则母线与高的夹角是( )
| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
12.不等式2x-7<5-2x的非负整数解有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.下列说法正确的是( )
| A. | 有两个角为直角的四边形是矩形 | B. | 矩形的对角线相等 | ||
| C. | 平行四边形的对角线相等 | D. | 对角线互相垂直的四边形是菱形 |
7.与不等式$\frac{x-3}{3}$<-1有相同的解集的是( )
| A. | 3x-3<4x-5 | B. | 3(x-3)<2(x-6)+3 | C. | 3x-9<4x-4 | D. | 2x-1<3 |
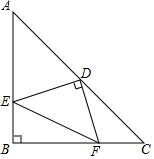 如图,在Rt△ABC中,AB=BC,∠B=90°,D是AC的中点,E、F分别是AB、BC上的点,且DE⊥DF,若AE=12,CF=5,求AC、EF的长.
如图,在Rt△ABC中,AB=BC,∠B=90°,D是AC的中点,E、F分别是AB、BC上的点,且DE⊥DF,若AE=12,CF=5,求AC、EF的长.