题目内容
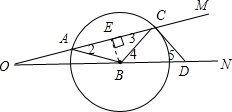
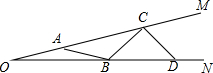 如图,在∠MON的两边依次截取OA=AB=BC=CD=2.
如图,在∠MON的两边依次截取OA=AB=BC=CD=2.(1)若DC⊥OM,求∠MON;
(2)以AB长为半径作⊙B,若AC=2
| 3 |
考点:切线的判定,等腰三角形的性质
专题:
分析:(1)利用等腰三角形的性质和三角形外角的性质,设出∠MON=α,然后找到各角之间的关系,求出∠MON的度数.
(2)要证CD是⊙B的切线,就要证∠BCD=90°,利用特殊角的三角函数值求出∠2=30°,再求出∠4和∠5都等于45°,从而证得∠BCD=90°.
(2)要证CD是⊙B的切线,就要证∠BCD=90°,利用特殊角的三角函数值求出∠2=30°,再求出∠4和∠5都等于45°,从而证得∠BCD=90°.
解答:解:如图,设∠MON=α
∵OA=AB
∴∠1=∠MON=α
∴∠2=∠MON+∠1=2α
又∵AB=BC
∴∠3=∠2=2α
∴∠4=∠MON+∠3=3α
又∵BC=CD
∴∠4=∠5=3α
∴∠MCD=∠MON+∠5=4α
又∵DC⊥OM
∴∠MCD=90°
∴4α=90°
α=22.5°
即∠MON=22.5°
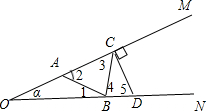
(2)如图过点B作BE⊥AC
∵AB=BC,BE⊥AC,AC=2
∴AE=CE=
AC=
又∵AB=2
∴cos∠2=
=
∴∠2=30°
又∵∠2=2∠MON
∴∠MON=15°
又∵∠4=∠5=3∠MON
∴∠4=∠5=45°
∴∠BCD=90°
∴CD是⊙B的切线.
∵OA=AB
∴∠1=∠MON=α
∴∠2=∠MON+∠1=2α
又∵AB=BC
∴∠3=∠2=2α
∴∠4=∠MON+∠3=3α
又∵BC=CD
∴∠4=∠5=3α
∴∠MCD=∠MON+∠5=4α
又∵DC⊥OM
∴∠MCD=90°
∴4α=90°
α=22.5°
即∠MON=22.5°

(2)如图过点B作BE⊥AC
∵AB=BC,BE⊥AC,AC=2
| 3 |
∴AE=CE=
| 1 |
| 2 |
| 3 |
又∵AB=2
∴cos∠2=
| AE |
| AB |
| ||
| 2 |
∴∠2=30°
又∵∠2=2∠MON
∴∠MON=15°
又∵∠4=∠5=3∠MON
∴∠4=∠5=45°
∴∠BCD=90°
∴CD是⊙B的切线.

点评:这道题主要考查等腰三角形的性质和切线的判定定理,并会熟练的应用,体现数形结合思想的重要性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知一次函数y=kx+b的图象如图,则关于x的不等式k(x-4)-2b>0的解集为( )
已知一次函数y=kx+b的图象如图,则关于x的不等式k(x-4)-2b>0的解集为( )| A、x>-2 | B、x<-2 |
| C、x>2 | D、x<3 |
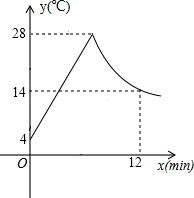 如图所示,制作某种食品的同时需将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟.据了解,该材料在加热过程中温度y与时间x成一次函数关系.已知该材料在加热前的温度为4℃,加热一段时间使材料温度达到28℃时停止加热,停止加热后,材料温度逐渐下降,这时温度y与时间x成反比例函数关系,已知当第12分钟时,材料温度是14℃.
如图所示,制作某种食品的同时需将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟.据了解,该材料在加热过程中温度y与时间x成一次函数关系.已知该材料在加热前的温度为4℃,加热一段时间使材料温度达到28℃时停止加热,停止加热后,材料温度逐渐下降,这时温度y与时间x成反比例函数关系,已知当第12分钟时,材料温度是14℃.