题目内容
已知等边三角形ABC内接于⊙O,P为⊙O上异于A、B、C的动点.当点P为弦BC所对的劣弧上一点时(如图),连接PA、PB、PC,
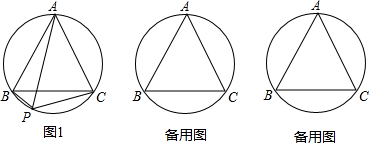
(1)求证:PB+PC=PA;
(2)当点P为弦BC所对的优弧上一点时,连接PA、PB、PC,猜想PA、PB和PC的数量关系为: ,不必证明;
(3)⊙O半径为4,当PB=2时,求PA的长.

(1)求证:PB+PC=PA;
(2)当点P为弦BC所对的优弧上一点时,连接PA、PB、PC,猜想PA、PB和PC的数量关系为:
(3)⊙O半径为4,当PB=2时,求PA的长.
考点:全等三角形的判定与性质,等边三角形的性质,圆周角定理,相似三角形的判定与性质
专题:
分析:(1)在PA上截取PD=PC,可证明△ACD≌△BCP,则AD=PB,从而得出PA=PB+PC;
(2)当点P为弦BC所对的优弧上一点时,相当于P点在弦AB所对的劣弧
上,所以有PC=PA+PB,或相当于P点在弦AC所对的
上,所以有PB=PA+PC.
(3)根据⊙O的半径求出圆内接等边三角形的边长,然后根据余弦定理求得PA的长.
(2)当点P为弦BC所对的优弧上一点时,相当于P点在弦AB所对的劣弧
 |
| AB |
 |
| AC |
(3)根据⊙O的半径求出圆内接等边三角形的边长,然后根据余弦定理求得PA的长.
解答:(1)证明:连结CD.在PA上截取PD=PC
∵AB=AC=BC,
∴∠APB=∠APC=60°,
∴△PCD为等边三角形,
∴∠PCD=∠ACB=60°,CP=CD,
∴∠PCD-∠DCB=∠ACB-∠DCB,即∠ACD=∠BCP,
在△ACD和△BCP中,
∴△ACD≌△BCP(SAS),
∴AD=PB,
∵PA=AD+DP,DP=PC,
∴PA=PB+PC
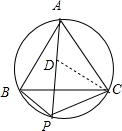
(2)解:PC=PA+PB或PB=PA+PC.
(3)解:如上图
∵△ABC都为等边三角形,⊙O半径为4,
∴AB=BC=AC=4
,
∵∠APB=∠ACB=60°,PB=2
根据余弦定理可知:PA2+PB2-AB2=2PA×PB•COS∠APB,
整理得PA2-2PA-44=0,
解得PA=1+3
或PA=1-3
(舍去)
∴PA=1+3
∵AB=AC=BC,
∴∠APB=∠APC=60°,
∴△PCD为等边三角形,
∴∠PCD=∠ACB=60°,CP=CD,
∴∠PCD-∠DCB=∠ACB-∠DCB,即∠ACD=∠BCP,
在△ACD和△BCP中,
|
∴△ACD≌△BCP(SAS),
∴AD=PB,
∵PA=AD+DP,DP=PC,
∴PA=PB+PC

(2)解:PC=PA+PB或PB=PA+PC.
(3)解:如上图
∵△ABC都为等边三角形,⊙O半径为4,
∴AB=BC=AC=4
| 3 |
∵∠APB=∠ACB=60°,PB=2
根据余弦定理可知:PA2+PB2-AB2=2PA×PB•COS∠APB,
整理得PA2-2PA-44=0,
解得PA=1+3
| 5 |
| 5 |
∴PA=1+3
| 5 |
点评:本题考查了全等三角形的判定和性质,相似三角形的判定和性质,圆周角的定理、等边三角形的性质以及余弦定理是一个综合题,有一定难度.

练习册系列答案
相关题目
2014年2月我国出口1141亿美元,进口1370.8亿美元,贸易逆差229.8亿美元,用科学记数法表示-229.8亿美元(保留3个有效数字)( )
| A、-2.29×1010 |
| B、-2.30×1010 |
| C、-2.3×109 |
| D、-2.30×109 |

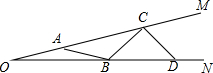 如图,在∠MON的两边依次截取OA=AB=BC=CD=2.
如图,在∠MON的两边依次截取OA=AB=BC=CD=2.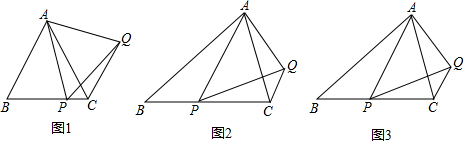
 如图,在平行四边形ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A,E之间,连接CE、CF、EF,有下列四个结论:
如图,在平行四边形ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A,E之间,连接CE、CF、EF,有下列四个结论: