题目内容
6.如果关于x的一元二次方程x2+2(k+3)x+k2+3=0有两个实数根α,β,那么(α-1)2+(β-1)2的最小值是多少?分析 根据根与系数的关系得到α+β=-2(k+3),αβ=k2+3,结合根的判别式得到k的取值范围,所以将其代入所求的代数式得到:(α-1)2+(β-1)2=(α+β)2-2(α+β)-2αβ+2=2(k+7)2-48,根据二次函数在定义域内的最值的求法进行解答.
解答 解:∵x2+2(k+3)x+k2+3=0有两个实数根α,β,
∴α+β=-2(k+3),αβ=k2+3,△=4(k+3)2-4(k2+3)≥0,
解得k≥-1.
∴(α-1)2+(β-1)2
=α2-2α+1+β2-2β+1,
=(α+β)2-2(α+β)-2αβ+2,
=4(k+3)2+4(k+3)-2(k2+3)+2,
=2k2+28k+44,
=2(k+7)2-54,
当k=-1时,(α-1)2+(β-1)2的最小值是:2(-1+7)2-54=18.
点评 本题考查了根与系数的关系,二次函数的最值.将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.

练习册系列答案
相关题目
18.某校八年级五班有7个合作学习小组,各学习小组的人数分别为:5,5,6,x,7,7,6,已知这组数据的平均数是6,则这组数据的众数和中位数分别是( )
| A. | 7,6 | B. | 6,6 | C. | 5,5 | D. | 7,7 |
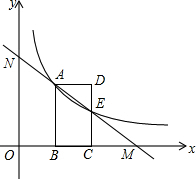 如图,在平面直角坐标系中,矩形ABCD的顶点B,C在x轴上,A,D在第一象限,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A,交CD于点E,OB=2,AB=3.
如图,在平面直角坐标系中,矩形ABCD的顶点B,C在x轴上,A,D在第一象限,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A,交CD于点E,OB=2,AB=3.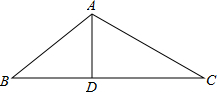 如图,D为△ABC的BC边上的一点,AB=10,AD=6,DC=2AD,BD=$\frac{2}{3}$DC.
如图,D为△ABC的BC边上的一点,AB=10,AD=6,DC=2AD,BD=$\frac{2}{3}$DC. 如图,在平面直角坐标系中,四边形OABC为菱形,已知A(-3,0),∠B=60°,求B,C两点的坐标.
如图,在平面直角坐标系中,四边形OABC为菱形,已知A(-3,0),∠B=60°,求B,C两点的坐标.