题目内容
11.已知二次函数y=x2-2ax+3(1)当x≥-2时,y随x的增大而增大,试求a的范围;
(2)当2<x<4时,y<0都成立,试求a的范围;
(3)当-1<x<4时,y>0都成立,试求a的范围.
分析 (1)根据二次函数的性质,利用二次函数的对称轴不大于1列式计算即可得解;
(2)把x=2和x=4代入y=x2-2ax+3,由y<0都成立,列不等式组即可解答;
(3)把x=-1和x=4代入y=x2-2ax+3,由y>0都成立,列不等式组即可解答.
解答 解:(1)抛物线的对称轴为直线x=a,
∵当x≥-2时,y的值随x值的增大而增大,
∴a≤-2,
(2)∵当2<x<4时,y<0都成立,
∴当x=2时,y=4-4a+3=7-4a≤0,
解得:a≥$\frac{7}{4}$;
当x=4时,y=16-8a+3=19-8a≤0,
解得:a≥$\frac{19}{8}$;
∴a≥$\frac{19}{8}$;
(3)∵-1<x<4时,y>0都成立,
∴当x=-1时,y=1+2a+3=4+2a≥0,
解得:a≥-2,
当x=4时,y=16-8a+3=19-8a≥0,
解得:a≤$\frac{19}{8}$,
∴-2≤a≤$\frac{19}{8}$.
点评 本题考查了二次函数的性质,熟练掌握二次函数的增减性,根据自变量的取值范围以及函数值与0的关系列出不等式(组)是解决问题的关键.

练习册系列答案
相关题目
20.下列二元一次方程组无解的是( )
| A. | $\left\{\begin{array}{l}{5x-3y=16}\\{3x-5y=0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=5}\\{2x-y=1}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{3x-y=1}\\{y=2x}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-y=2}\\{2x-2y=-4}\end{array}\right.$ |
1.为保护生态环境,陕西省某县响应国家“退耕还林”号召,将某一部分耕地改为林地,改变后,林地面积和耕地面积共有180平方千米,耕地面积是林地面积的25%,为求改变后林地面积和耕地面积各多少平方千米.设改变后耕地面积x平方千米,林地地面积y平方千米,根据题意,列出如下四个方程组,其中正确的是( )
| A. | $\left\{\begin{array}{l}x+y=180\\ y=x•25%\end{array}\right.$ | B. | $\left\{\begin{array}{l}x+y=180\\ x=y•25%\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}x+y=180\\ x-y=25%\end{array}\right.$ | D. | $\left\{\begin{array}{l}x+y=180\\ y-x=25%\end{array}\right.$ |
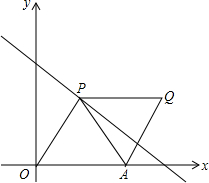 如图,点P(m,n)是直线y=-x+8上的动点,点A的坐标为(6,0),以PA为对角线,作面积为S的平行四边形OPQA.
如图,点P(m,n)是直线y=-x+8上的动点,点A的坐标为(6,0),以PA为对角线,作面积为S的平行四边形OPQA.