题目内容
18. 如图,△PAO和△PBQ是等边三角形,连接AB,OQ,求证:AB=OQ.
如图,△PAO和△PBQ是等边三角形,连接AB,OQ,求证:AB=OQ.
分析 由SAS证明△APB≌△OPQ,得出对应边相等即可.
解答 证明:∵△PAO和△PBQ是等边三角形,
∴OA=OP,PB=PQ,∠APO=∠BPQ=60°,
∴∠APB=∠OPQ,
在△APB和△OPQ中,$\left\{\begin{array}{l}{AP=OP}&{\;}\\{∠APB=∠OPQ}&{\;}\\{PB=PQ}&{\;}\end{array}\right.$,
∴△APB≌△OPQ(SAS),
∴AB=OQ.
点评 本题考查了全等三角形的判定与性质、等边三角形的性质,熟练掌握全等三角形的判定是解题的关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
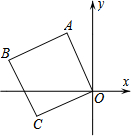 如图,平面直角坐标系中有一正方形OABC,点C的坐标为(-4,-2).
如图,平面直角坐标系中有一正方形OABC,点C的坐标为(-4,-2).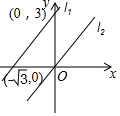 如图,直线L1过点(0,3),(-$\sqrt{3}$,0).
如图,直线L1过点(0,3),(-$\sqrt{3}$,0).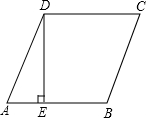 如图所示,在菱形ABCD中,DE⊥AB于E,BE=16cm,sinA=$\frac{12}{13}$,求此菱形的周长.
如图所示,在菱形ABCD中,DE⊥AB于E,BE=16cm,sinA=$\frac{12}{13}$,求此菱形的周长.