题目内容
6.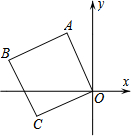 如图,平面直角坐标系中有一正方形OABC,点C的坐标为(-4,-2).
如图,平面直角坐标系中有一正方形OABC,点C的坐标为(-4,-2).(1)求点A的坐标.
(2)线段BO的长度.
分析 (1)过点A作AE⊥y轴,垂足为E,过点C作CD⊥y轴,垂足为D,由△AEO≌△ODC,推出OE=CD=4,AE=OD=2,即可解决问题.
(2)同理可证△BFC≌△△ODC,推出CF=OD=2,BF=CD=4,推出B(-6,2),利用两点间距离公式计算即可.
解答 解:(1)过点A作AE⊥y轴,垂足为E,过点C作CD⊥y轴,垂足为D,
∵四边形ABCD是正方形,
∴OA=OC,∠AOC=90°,
∴∠AOE+∠COD=90°,∠AOE+∠OAE=90°,
∴∠COD=∠OAE,
在△AEO和△ODC中,
$\left\{\begin{array}{l}{∠AEO=∠CDO=90°}\\{∠OAE=∠COD}\\{OA=OC}\end{array}\right.$
△AEO≌△ODC,
∴OE=CD=4,AE=OD=2,
∴A(-2,4).
(2)同理可证△BFC≌△△ODC,
∴CF=OD=2,BF=CD=4,
∴B(-6,2),
∴OB=$\sqrt{{6}^{2}+{2}^{2}}$=2$\sqrt{10}$.
点评 本题考查正方形的性质、坐标与图形的性质、两点间距离公式、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
17.为增强公民节水意识,合理利用水资源,某市采用“阶梯收费”,标准如下表:
譬如:某用户2月份用水9m3,则应缴水费:2×6+4×(9-6)=24(元)
(1)某用户3月用水15m3应缴水费多少元?
(2)已知某用户4月份缴水费20元,求该用户4月份的用水量;
(3)如果该用户5、6月份共用水20m3 (6月份用水量超过5月份用水量),共交水费64元,则该户居民5、6月份各用水多少立方米?
| 用水量 | 单价 |
| 不超过6m3的部分 | 2元/m3 |
| 超过6m3不超过10m3的部分 | 4元/m3 |
| 超出10m3的部分 | 8元/m3 |
(1)某用户3月用水15m3应缴水费多少元?
(2)已知某用户4月份缴水费20元,求该用户4月份的用水量;
(3)如果该用户5、6月份共用水20m3 (6月份用水量超过5月份用水量),共交水费64元,则该户居民5、6月份各用水多少立方米?
16.某工程要在x天内完成,现由甲先做3天,乙再参加合做,正好如期完成.若甲独做需12天完成,乙独做需8天完成,则下列方程正确的是( )
| A. | $\frac{x}{12}$+$\frac{x-3}{8}$=1 | B. | $\frac{x+3}{12}$+$\frac{x-3}{8}$=1 | C. | $\frac{x}{12}$+$\frac{x}{8}$=1 | D. | $\frac{x+3}{12}$+$\frac{x}{8}$=1 |

 如图,△PAO和△PBQ是等边三角形,连接AB,OQ,求证:AB=OQ.
如图,△PAO和△PBQ是等边三角形,连接AB,OQ,求证:AB=OQ.