题目内容
17. 如图,点G是Rt△ABC的重心,过点G作矩形GECF,当GF:GE=1:2时,则∠A的正切值.
如图,点G是Rt△ABC的重心,过点G作矩形GECF,当GF:GE=1:2时,则∠A的正切值.
分析 根据重心定理可知,AG:GD=2:1,由GF:GE=1:2,从而可以得到各边的关系,从而可以解答本题.
解答 解:如下图所示,连接AG并延长与BC交于点D.
∵点G是Rt△ABC的重心,GF:GE=1:2,
∴AG:AD=AE:AC=GE:DC=2:3,BC=2CD.
设GF=a,则GE=2a.
∴CD=3a,AC=3a,BC=6a.
∴tanA=$\frac{BC}{AC}=\frac{6a}{3a}=2$.
即∠A的正切值是2.
点评 本题考查解直角三角形和三角形的重心,解题的关键是明确重心定理,找准各边的关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.下列语句中,正确的是( )
| A. | 由有一个公共端点且相等的两条线段组成的图形一定是轴对称图形 | |
| B. | 由有一个公共端点且不相等的两条线段组成的图形一定不是轴对称图形 | |
| C. | 锐角三角形一定是轴对称图形 | |
| D. | 锐角三角形一定不是轴对称图形 |
12.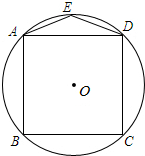 如图,正方形ABCD内接于⊙O,点E在劣弧$\widehat{AD}$上,则∠AED等于( )
如图,正方形ABCD内接于⊙O,点E在劣弧$\widehat{AD}$上,则∠AED等于( )
 如图,正方形ABCD内接于⊙O,点E在劣弧$\widehat{AD}$上,则∠AED等于( )
如图,正方形ABCD内接于⊙O,点E在劣弧$\widehat{AD}$上,则∠AED等于( )| A. | 100° | B. | 120° | C. | 135° | D. | 150° |
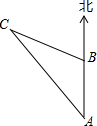 如图,上午8时,一艘轮船从A处出发以每小时20海里的速度向正北航行,10时到达B处,则轮船在A处测得灯塔C在北偏西36°,航行到B处时,又测得灯塔C在北偏西72°,则从B到灯塔C的距离是40海里.
如图,上午8时,一艘轮船从A处出发以每小时20海里的速度向正北航行,10时到达B处,则轮船在A处测得灯塔C在北偏西36°,航行到B处时,又测得灯塔C在北偏西72°,则从B到灯塔C的距离是40海里.