题目内容
17.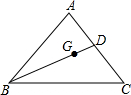 如图,BD是△ABC的中线,G为△ABC的重心,设$\overrightarrow{BA}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$的线性组合表示向量$\overrightarrow{GB}$.
如图,BD是△ABC的中线,G为△ABC的重心,设$\overrightarrow{BA}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,试用$\overrightarrow{a}$,$\overrightarrow{b}$的线性组合表示向量$\overrightarrow{GB}$.
分析 根据向量的平行四边形法则,可得$\overrightarrow{BD}$,根据三角形的重心性质,可得$\overrightarrow{BG}$,根据相反向量的定义,可得答案.
解答 解:由向量的平等四边形法则知
$\overrightarrow{BD}$=$\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{b}$).
由三角形重心性质知
$\overrightarrow{BG}$=$\frac{2}{3}$$\overrightarrow{BD}$=$\frac{1}{3}$($\overrightarrow{a}$+$\overrightarrow{b}$).
由相反向量知
$\overrightarrow{GB}$=-$\frac{1}{3}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$.
点评 本题考查了平面向量,利用了向量的平行四边形法则,三角形的重心性质,相反向量.

练习册系列答案
相关题目
8.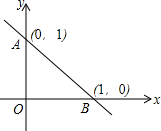 如图一次函数y=kx+b的图象与y轴交于点(0,1),与x轴交于点(1,0),则关于x的不等式kx+b>1的解集是( )
如图一次函数y=kx+b的图象与y轴交于点(0,1),与x轴交于点(1,0),则关于x的不等式kx+b>1的解集是( )
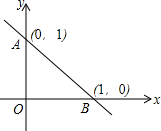 如图一次函数y=kx+b的图象与y轴交于点(0,1),与x轴交于点(1,0),则关于x的不等式kx+b>1的解集是( )
如图一次函数y=kx+b的图象与y轴交于点(0,1),与x轴交于点(1,0),则关于x的不等式kx+b>1的解集是( )| A. | x>0 | B. | x<0 | C. | x>1 | D. | x<1 |
5.筷子中有同样大小的红球1个、绿球2个,随机提出1个小球记下颜色后放回,再随机摸出1个,则两次摸到的球都是绿球的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{1}{9}$ |
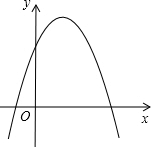 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则:a<0;b>0;c>0;b2-4ac>0.
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则:a<0;b>0;c>0;b2-4ac>0.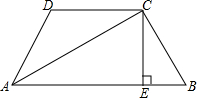 如图,四边形ABCD中,CE⊥AB于E,将①AC平分∠BAD;②CB=CD;③∠B+∠ADC=180°;④AB+AD=2AE中的任意两个作为条件,都可得出另两个结论,请你一一探究,并任选一种情形予以证明.
如图,四边形ABCD中,CE⊥AB于E,将①AC平分∠BAD;②CB=CD;③∠B+∠ADC=180°;④AB+AD=2AE中的任意两个作为条件,都可得出另两个结论,请你一一探究,并任选一种情形予以证明.