题目内容
10.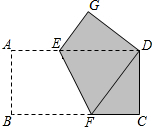 如图,矩形ABCD中,AB=2,AD=4,将矩形沿FE折叠,使点B与点D重合,点A的对应点是点G,则图中阴影部分的面积为$\frac{11}{2}$.
如图,矩形ABCD中,AB=2,AD=4,将矩形沿FE折叠,使点B与点D重合,点A的对应点是点G,则图中阴影部分的面积为$\frac{11}{2}$.
分析 根据矩形的性质,可得BC与AD的关系,根据翻折的性质,AB与DG的关系,根据全等三角形的判定与性质,可得EG与CF的关系,根据勾股定理,可得CF的长,根据面积的和差,可得答案.
解答 解:∵四边形ABCD是矩形,
∴BC||AD,
∴∠BFE=∠DEF,
∵将矩形纸片沿EF折叠,使点B与点D重合,
∴∠BFE=∠EFD,
∴∠DEF=∠DFE,
∴DE=DF.
∵将矩形纸片沿EF折叠,使点B与点D重合,
∴DG=AB=2.
∵四边形ABCD是矩形,
∴AB=CD
∴DG=CD.
在Rt△CDF和Rt△DGE中,$\left\{\begin{array}{l}{∠GDE=∠CDF}\\{∠G=∠C=90°}\\{DG=CD}\end{array}\right.$,
∴△CDF∽△DGE,
∴EG=CF,DE=CF,
设BF=DF=x,则CF=EG=(4-x),
在Rt△CDF中,DF2=CF2+CD2,
即(4-x)2+22=x2
x=$\frac{5}{2}$,CF=$\frac{3}{2}$.
∵DE=BF=$\frac{5}{2}$,
∴AE=CF=$\frac{3}{2}$,
∴S着色=S四边形CDEF+S△DEG,
=$\frac{1}{2}$×($\frac{3}{2}$+$\frac{5}{2}$)×2+$\frac{1}{2}$×2×$\frac{3}{2}$
=4+$\frac{3}{2}$
=$\frac{11}{2}$.
故答案为:$\frac{11}{2}$.
点评 本题考查了翻折的性质,利用了矩形的性质,翻折的性质,利用勾股定理得出BE的长是解题关键,又利用了面积的和差.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
20.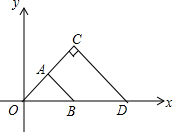 如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD,若B(1,0),则C点的坐标为( )
如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD,若B(1,0),则C点的坐标为( )
 如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD,若B(1,0),则C点的坐标为( )
如图,△OAB与△OCD是以点O为位似中心的位似图形,相似比为1:2,∠OCD=90°,CO=CD,若B(1,0),则C点的坐标为( )| A. | (1,2) | B. | ($\sqrt{2},\sqrt{2}$) | C. | (1,1) | D. | (2,1) |
18.无论x为何值,下列各分式中总有意义的是( )
| A. | $\frac{1}{2x+1}$ | B. | $\frac{x}{2x+1}$ | C. | $\frac{3x+1}{{x}^{2}}$ | D. | $\frac{{x}^{2}}{2{x}^{2}+1}$ |
5. 如图,把一张矩形纸片对折两次得到四个小矩形,如果每个小矩形都与原矩形相似,则原矩形纸片的长与宽之比为( )
如图,把一张矩形纸片对折两次得到四个小矩形,如果每个小矩形都与原矩形相似,则原矩形纸片的长与宽之比为( )
 如图,把一张矩形纸片对折两次得到四个小矩形,如果每个小矩形都与原矩形相似,则原矩形纸片的长与宽之比为( )
如图,把一张矩形纸片对折两次得到四个小矩形,如果每个小矩形都与原矩形相似,则原矩形纸片的长与宽之比为( )| A. | $\sqrt{2}$:1 | B. | 2:1 | C. | 3:1 | D. | 4:1 |
15.观察分析下列数据,寻找规律:$\sqrt{3}$,$\sqrt{6}$,3,$2\sqrt{3}$,$\sqrt{15}$,$3\sqrt{2}$,…那么第25个数据应是5$\sqrt{3}$.
19.若n满足(n-2015)2+(2016-n)2=1,则(n-2015)(2016-n)=( )
| A. | -1 | B. | 0 | C. | $\frac{1}{2}$ | D. | 1 |
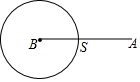 如图,动点S从点A出发,沿线段AB运动至点B后,立即按原路返回,点S在运动过程中速度不变,则以点B为圆心,线段BS长为半径的圆的面积m与点S的运动时间t之间的函数关系图象大致为( )
如图,动点S从点A出发,沿线段AB运动至点B后,立即按原路返回,点S在运动过程中速度不变,则以点B为圆心,线段BS长为半径的圆的面积m与点S的运动时间t之间的函数关系图象大致为( )