题目内容
12.已知一个圆心角为270°扇形工件,未搬动前如图所示,A、B两点触地放置,搬动时,先将扇形以B为圆心,作如图所示的无滑动翻转,再使它紧贴地面滚动,当A、B两点再次触地时停止,半圆的直径为8m,则圆心O所经过的路线长是8πm(结果保留π).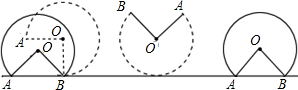
分析 O经过的路线是两个半径是4m,圆心角的45°的弧,平移的距离是半径长是4m,圆心角是270°的弧长,二者的和就是所求的路线长.
解答  解:∠AOB=360°-270°=90°,则∠ABO=45°,
解:∠AOB=360°-270°=90°,则∠ABO=45°,
则∠OBC=45°,
O旋转的长度是:2×$\frac{45π×4}{180}$=2πm;
O移动的距离是:$\frac{270π×4}{180}$=6πm,
则圆心O所经过的路线长是:2π+6π=8πm,
故答案为:8π.
点评 本题考查了弧长的计算公式,正确理解O经过的路线是关键.

练习册系列答案
相关题目
4.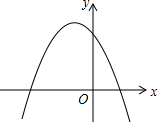 函数y=ax2+bx+c(a≠0)的图象如图所示,那么关于x的方程ax2+bx+c=0的根的情况是( )
函数y=ax2+bx+c(a≠0)的图象如图所示,那么关于x的方程ax2+bx+c=0的根的情况是( )
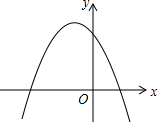 函数y=ax2+bx+c(a≠0)的图象如图所示,那么关于x的方程ax2+bx+c=0的根的情况是( )
函数y=ax2+bx+c(a≠0)的图象如图所示,那么关于x的方程ax2+bx+c=0的根的情况是( )| A. | 有两个不相等的实数根 | B. | 有两个同号的实数根 | ||
| C. | 有两个相等实数根 | D. | 无实数根 |
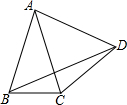 如图,△ABC中,AB=AC,∠BAC=50°,边AB绕点A逆时针旋转m°,(0<m<360)得到线段AD,连接BD、DC.若△BDC为等腰三角形,则m所有可能的取值是25或100或205或310.
如图,△ABC中,AB=AC,∠BAC=50°,边AB绕点A逆时针旋转m°,(0<m<360)得到线段AD,连接BD、DC.若△BDC为等腰三角形,则m所有可能的取值是25或100或205或310.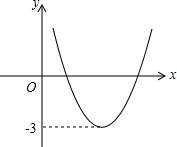 如图,已知函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c+2=0的根的情况是有两个同号不等实数根.
如图,已知函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c+2=0的根的情况是有两个同号不等实数根. 如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC,若∠AEB=50°,求∠EBC的度数是25°.
如图,△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC,若∠AEB=50°,求∠EBC的度数是25°.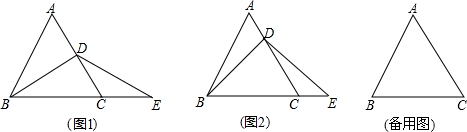
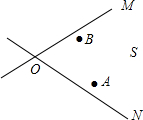 如图,学校要在两条小路OM和ON之间的S区域规划修建一处“英语角”,按照设计要求,英语角C到两栋教学楼A,B的距离必须相等,到两条小路的距离也必须相等,则“英语角”应修建在什么位置?请在图上标出它的位置.(尺规作图,保留痕迹)
如图,学校要在两条小路OM和ON之间的S区域规划修建一处“英语角”,按照设计要求,英语角C到两栋教学楼A,B的距离必须相等,到两条小路的距离也必须相等,则“英语角”应修建在什么位置?请在图上标出它的位置.(尺规作图,保留痕迹)