题目内容
9.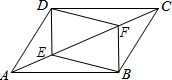 已知:如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF.
已知:如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF.求证:四边形DEBF是平行四边形.
证明:∵四边形ABCD是平行四边形
∴AD=BC,AD∥BC
∠DAE=∠DCF.
又AE=CF,
∴△ADE≌△CBF
∴DE=BF,∠DEA=∠CFB.
∴∠DEF=∠BFA.
∴DE∥BF
∴四边形ABCD是平行四边形.有一组对边平行且相等的四边形是平行四边形.
分析 可由题中条件求解△ADE≌△CBF,得出∠AED=∠CFB,即∠DEC=∠BFA,进而可求得结论.
解答 证明:∵四边形ABCD是平行四边形,
∴AD=BC,AB∥CD,
∴∠BAE=∠DCF,
在△ADE和△CBF中,
$\left\{\begin{array}{l}{AD=BC}\\{∠BAE=∠DCF}\\{AE=CF}\end{array}\right.$,
∴△ADE≌△CBF(SAS),
∴∠AED=∠CFB,BF=DE
∴∠DEC=∠BFA,
∴DE∥BF,
∴四边形DEBF是平行四边形.
故答案为:BC,DCF,CBF,BF,CFB,BFA,有一组对边平行且相等的四边形是平行四边形.
点评 本题主要考查了平行四边形的性质及全等三角形的判定及性质,能够运用其性质解决一些简单的证明问题.

练习册系列答案
相关题目
17.α,β是方程x2+2x-5=0的两个实数根,则αβ的值为( )
| A. | 5 | B. | -5 | C. | 2 | D. | -2 |
14.将一个平行四边形的纸片折一次,使得折痕平分这个平行四边形的面积,则这样的折纸方法共有( )
| A. | 1种 | B. | 2种 | C. | 3种 | D. | 无数种 |
 某河道A,B两个码头之间有客轮和货轮通行,某天,客轮从A码头出发,匀速行驶到B码头,同时货轮从B码头出发,运送一批建材匀速行驶到A码头.两船距B码头的距离y(千米)与行驶时间x(分钟)之间的函数关系图象如图所示.
某河道A,B两个码头之间有客轮和货轮通行,某天,客轮从A码头出发,匀速行驶到B码头,同时货轮从B码头出发,运送一批建材匀速行驶到A码头.两船距B码头的距离y(千米)与行驶时间x(分钟)之间的函数关系图象如图所示. 如图所示,AB与CD交于O,若∠COA=50°,则∠BOD=50°.
如图所示,AB与CD交于O,若∠COA=50°,则∠BOD=50°.
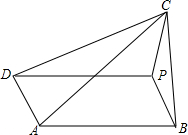 四边形ABCD内部存在一点P,使得ABPD为平行四边形.求证:若∠CBP=∠CDP,则∠ACD=∠BCP,反之亦然.
四边形ABCD内部存在一点P,使得ABPD为平行四边形.求证:若∠CBP=∠CDP,则∠ACD=∠BCP,反之亦然.