题目内容
4.如果$\sqrt{a-6}+{(b-3)^2}=0$,则$\sqrt{a+b}$的值为3.分析 根据非负数的性质列出方程求出a、b的值,代入所求代数式计算即可.
解答 解:∵$\sqrt{a-6}+{(b-3)^2}=0$,
∴a-6=0,b-3=0,
∴a=6,b=3,
∴$\sqrt{a+b}$=$\sqrt{6+3}$=$\sqrt{9}$=3.
故答案为3.
点评 本题考查了非负数的性质:算术平方根、偶次方,几个非负数的和为0时,这几个非负数都为0.

练习册系列答案
相关题目

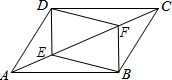 已知:如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF.
已知:如图,E、F是平行四边形ABCD的对角线AC上的两点,AE=CF.
 老师出了如下的题:如图,要求在图中按下面的语言继续画图:(画图工具和方法不限)过A点画AD⊥BC于D,过D点画DE∥AB交AC于E,在线段AB上任取一点F,以F为顶点,FB为一边,画∠BFG=∠ADE,∠BFG的另一边FG与线段BC交于点G.请你按照上面画图时给出的条件说明FG⊥BC.
老师出了如下的题:如图,要求在图中按下面的语言继续画图:(画图工具和方法不限)过A点画AD⊥BC于D,过D点画DE∥AB交AC于E,在线段AB上任取一点F,以F为顶点,FB为一边,画∠BFG=∠ADE,∠BFG的另一边FG与线段BC交于点G.请你按照上面画图时给出的条件说明FG⊥BC.