题目内容
16.已知:$\frac{a}{4}$=$\frac{b}{3}$=$\frac{c}{2}$且a+3b-3c=14,求4a-3b+c的值.分析 设$\frac{a}{4}$=$\frac{b}{3}$=$\frac{c}{2}$=t,利用比例性质得a=4t,b=3t,c=2t,则4t+9t-6t=14,解得t=2,再用t表示4a-3b+c,然后把t=2代入计算即可.
解答 解:∵$\frac{a}{4}$=$\frac{b}{3}$=$\frac{c}{2}$=t,
∴a=4t,b=3t,c=2t,
∵a+3b-3c=14,
∴4t+9t-6t=14,解得t=2,
∴4a-3b+c=16t-9t+2t=9t=18.
点评 本题考查了解三元一次方程组:把解三元一次方程组的问题转化为解二元一次方程的问题.也考查了比例的性质.

练习册系列答案
相关题目
7.已知代数式m-n+1的值是8,那么代数式4m-4n+1的值是( )
| A. | 37 | B. | 25 | C. | 29 | D. | 0 |
8.若关于x的一元二次方程x2-2x+4-a=0有两个正实数根,则a的取值范围是( )
| A. | a<4 | B. | a>4 | C. | 3≤a≤4 | D. | 3≤a<4 |
 一几何体是由若干个相同的小立方块搭成的,它的主视图和左视图相同,且如图所示,则搭该几何体的小立方块最多几块?最少几块?
一几何体是由若干个相同的小立方块搭成的,它的主视图和左视图相同,且如图所示,则搭该几何体的小立方块最多几块?最少几块?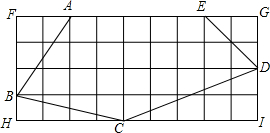 如图,每个小方格都是边长为1的正方形,计算五边形ABCDE的周长.
如图,每个小方格都是边长为1的正方形,计算五边形ABCDE的周长.