题目内容
15.已知直角梯形一腰长为10,此腰与底成45°角,那么另一腰长是( )| A. | 10 | B. | 5$\sqrt{2}$ | C. | 5$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
分析 作梯形的高线DE,根据等腰直角三角形求直角边DE=EC=5$\sqrt{2}$,再由两平行线的距离相等得:AB=5$\sqrt{2}$.
解答  解:过D作DE⊥BC于E,
解:过D作DE⊥BC于E,
∵∠C=45°,
∴△DEC是等腰直角三角形,
∵DC=10,
∴DE=EC=$\frac{10}{\sqrt{2}}$=5$\sqrt{2}$,
∵AD∥BC,AB⊥BC,
∴AB=DE=5$\sqrt{2}$;
故选B.
点评 本题考查了直角梯形的性质、等腰直角三角形的性质和判定、平行线的距离和勾股定理,得出△DEC是等腰直角三角形是本题的关键.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
20.已知三角形两边的长分别是3和7,则第三边的长可以是( )
| A. | 3 | B. | 6 | C. | 10 | D. | 16 |
5.某自行车厂计划一周生产自行车1400辆,平均每天生产200辆,但由于种种原因,实际每天生产量与计划量相比有出入,下表是某周的实际生产量与计划量的差值:
(1)根据记录的数据可知该厂星期四生产自行车多少辆?
(2)根据记录的数据可知该厂本周实际生产自行车多少辆?
(3)产量最多的一天比产量最少的一天多生产多少辆自行车?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 生产量与计划量的差值 | +5 | -2 | -4 | +13 | -10 | +14 | -9 |
(2)根据记录的数据可知该厂本周实际生产自行车多少辆?
(3)产量最多的一天比产量最少的一天多生产多少辆自行车?
 如图,用尺规作图在五边形ABCDE的边BC上找一点P,使∠APB=60°.(保留作图痕迹,不写作法)
如图,用尺规作图在五边形ABCDE的边BC上找一点P,使∠APB=60°.(保留作图痕迹,不写作法)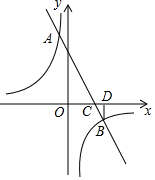 如图,已知一次函数y1=k1x+6与反比例函数y2=$\frac{{k}_{2}}{x}$相交于A、B,与x轴交于点C,过点B作BD⊥x轴于点D,已知sin∠DBC=$\frac{\sqrt{5}}{5}$,OC:CD=3:1.
如图,已知一次函数y1=k1x+6与反比例函数y2=$\frac{{k}_{2}}{x}$相交于A、B,与x轴交于点C,过点B作BD⊥x轴于点D,已知sin∠DBC=$\frac{\sqrt{5}}{5}$,OC:CD=3:1.
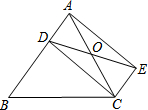 如图,点O为△ABC的边AC上一动点,经过点O的直线DE∥BC交AB于D,且OD=OE.
如图,点O为△ABC的边AC上一动点,经过点O的直线DE∥BC交AB于D,且OD=OE.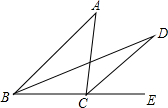 如图,在△ABC中,∠A=40°,BD,CD分别是∠ABC与外角∠ACE的平分线,并交于点D,则∠D的度数为20°.
如图,在△ABC中,∠A=40°,BD,CD分别是∠ABC与外角∠ACE的平分线,并交于点D,则∠D的度数为20°.