题目内容
7.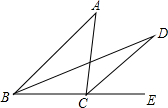 如图,在△ABC中,∠A=40°,BD,CD分别是∠ABC与外角∠ACE的平分线,并交于点D,则∠D的度数为20°.
如图,在△ABC中,∠A=40°,BD,CD分别是∠ABC与外角∠ACE的平分线,并交于点D,则∠D的度数为20°.
分析 根据角平分线的定义得到∠DCE=$\frac{1}{2}∠$ACE,∠DBC=$\frac{1}{2}∠$ABC,根据三角形的外角的性质计算即可.
解答 解:∵BD,CD分别是∠ABC与外角∠ACE的平分线,
∴∠DCE=$\frac{1}{2}∠$ACE,∠DBC=$\frac{1}{2}∠$ABC,
∵∠ACE-∠ABC=∠A=40°,
∴∠D=∠DCE-∠DBC=$\frac{1}{2}∠$A=20°,
故答案为:20°.
点评 本题考查的是三角形的外角的性质,掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键.

练习册系列答案
相关题目
15.已知直角梯形一腰长为10,此腰与底成45°角,那么另一腰长是( )
| A. | 10 | B. | 5$\sqrt{2}$ | C. | 5$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
2.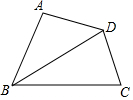 如图,在四边形ABCD中,∠A=90°,AD=4,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )
如图,在四边形ABCD中,∠A=90°,AD=4,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )
 如图,在四边形ABCD中,∠A=90°,AD=4,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )
如图,在四边形ABCD中,∠A=90°,AD=4,BC=5,对角线BD平分∠ABC,则△BCD的面积为( )| A. | 10 | B. | 12 | C. | 20 | D. | 无法确定 |
16.给出下列结论:
①任意两个等边三角形相似
②顶角对应相等的两个等腰三角形相似
③两条边对应成比例的两个直角三角形相似
其中正确的是( )
①任意两个等边三角形相似
②顶角对应相等的两个等腰三角形相似
③两条边对应成比例的两个直角三角形相似
其中正确的是( )
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
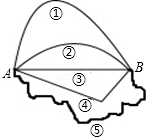 如图,从A地到B地共有五条路,人们常常选择第③条,请用几何知识解释原因两点之间,线段最短.
如图,从A地到B地共有五条路,人们常常选择第③条,请用几何知识解释原因两点之间,线段最短.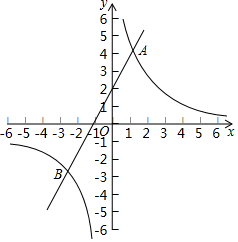 如图,直线y=2x+n与双曲线y=$\frac{m}{x}$(m≠0)交于A,B两点,且点A的坐标为(1,4).
如图,直线y=2x+n与双曲线y=$\frac{m}{x}$(m≠0)交于A,B两点,且点A的坐标为(1,4).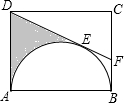 矩形ABCD中,AB=6,以AB为直径在矩形内作半圆,与DE相切于点E(如图),延长DE交BC于F,若BF=$\sqrt{3}$,则阴影部分的面积为9$\sqrt{3}$-3π.
矩形ABCD中,AB=6,以AB为直径在矩形内作半圆,与DE相切于点E(如图),延长DE交BC于F,若BF=$\sqrt{3}$,则阴影部分的面积为9$\sqrt{3}$-3π.