题目内容
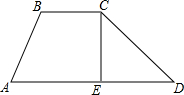 如图,水库大坝的横断面近似于梯形ABCD,迎水坡BC的倾斜角∠D=30°,背水坡AB的坡比为1.2:1,坝顶BC=6米,坝高CE=8米,求CD和AD的长.
如图,水库大坝的横断面近似于梯形ABCD,迎水坡BC的倾斜角∠D=30°,背水坡AB的坡比为1.2:1,坝顶BC=6米,坝高CE=8米,求CD和AD的长.考点:解直角三角形的应用-坡度坡角问题
专题:
分析:作BF⊥AD,垂足点F,得到两个直角三角形和一个矩形,利用相应的性质求解即可.
解答:解:作BF⊥AD,垂足点F,则四边形BCEF是矩形,

由题意得,BC=EF=6米,BF=CE=8米,斜坡AB的坡比为1.2:1,
在Rt△ABF中,
=
,
∴AF=
米.
在Rt△CED中,∠D=30°,
∴CD=2CE=16米,DE=CEcot∠D=8×
=
米,
∴AD=AF+EF+ED=
+6+
=
(米).
故CD长16米,AD长
米.

由题意得,BC=EF=6米,BF=CE=8米,斜坡AB的坡比为1.2:1,
在Rt△ABF中,
| BF |
| AF |
| 1.2 |
| 1 |
∴AF=
| 20 |
| 3 |
在Rt△CED中,∠D=30°,
∴CD=2CE=16米,DE=CEcot∠D=8×
| ||
| 3 |
8
| ||
| 3 |
∴AD=AF+EF+ED=
| 20 |
| 3 |
8
| ||
| 3 |
38+8
| ||
| 3 |
故CD长16米,AD长
38+8
| ||
| 3 |
点评:本题考查了解直角三角形的应用-坡度坡角问题,解答本题的关键是构造直角三角形和矩形,注意理解坡度与坡角的定义.

练习册系列答案
相关题目
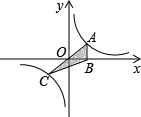 如图,正比例函数y=x与反比例函数y=
如图,正比例函数y=x与反比例函数y= 如图,A、B是双曲线y=
如图,A、B是双曲线y= 已知:如图,AB∥CD,AD∥BC,求证:AB=CD,AD=BC.
已知:如图,AB∥CD,AD∥BC,求证:AB=CD,AD=BC.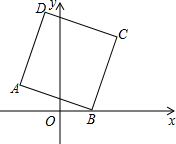 如图,在平面直角坐标系xOy中,点B是x轴上一动点,且点A(-3,2),连接AB,以AB为边向上作正方形ABCD.
如图,在平面直角坐标系xOy中,点B是x轴上一动点,且点A(-3,2),连接AB,以AB为边向上作正方形ABCD.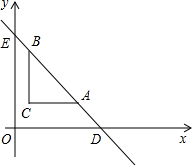 如图,在平面直角坐标系中,过点C(1,2)分别作x轴、y轴的平行线,交直线DE于A、B两点,点D的坐标是(6,0),点E的坐标是(0,6).
如图,在平面直角坐标系中,过点C(1,2)分别作x轴、y轴的平行线,交直线DE于A、B两点,点D的坐标是(6,0),点E的坐标是(0,6).