题目内容
18.已知△ABC中,D、E分别是BC、AC的中点,AB为⊙O的直径.(1)当⊙O经过点D,且AC与⊙O相切时,试判断△ABC的形状,并证明你的结论;
(2)当⊙O与△ABC的边有怎样的位置关系时,△ABC是等腰三角形而不是直角三角形?(不用证明)
(3)当⊙O与△ABC的边有怎样的位置关系时,△ABC是等边三角形?请你先把图形画出来再证明.
分析 (1)根据切线的性质定理以及圆周角的性质证明AC⊥AB即可证得;
(2)当满足(1)时是等腰直角三角形,
解答 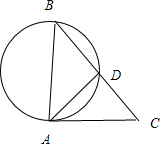 解:(1)△ABC是等腰直角三角形.
解:(1)△ABC是等腰直角三角形.
理由是:连接AD.
∵AB是圆的切线,
∴∠ADB=90°,即AD⊥BC.
∵D是BC的中点,
∴AC=AB.
∵AC是切线,AB是直径,
∴AC⊥AB,
∴△ABC是等腰直角三角形;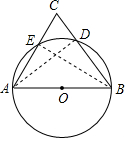
(2)当圆与AC、BC相交,且D、E中至少有一点在圆上时,△ABC是等腰三角形,而不是直角三角形;
(3)当圆与AC、BC相交,且D、E同时在圆上时,△ABC是等边三角形.
证明:连接DA、EB.
∵AB是圆的切线,
∴∠ADB=90°,即AD⊥BC.
∵D是BC的中点,
∴AC=AB.
同理AB=BC,
∴AB=BC=CA.
点评 本题考查了圆周角的相关知识、线段的垂直平分线的性质和判定.正确理解题意并作出图形是解决本题的关键.

练习册系列答案
相关题目
9.已知x≠y,下列各式与$\frac{x-y}{x+y}$相等的是( )
| A. | $\frac{(x-y)+5}{(x+y)+5}$ | B. | $\frac{2x-y}{2x+y}$ | C. | $\frac{(x-y)^{2}}{{x}^{2}-{y}^{2}}$ | D. | $\frac{{x}^{2}-{y}^{2}}{{x}^{2}+{y}^{2}}$ |
 如图,在由大小相同的小正方形拼成的正方形网格中,请在图中画出所有符合要求的线段,使它与线段AB、CD构成的图形为轴对称图形.
如图,在由大小相同的小正方形拼成的正方形网格中,请在图中画出所有符合要求的线段,使它与线段AB、CD构成的图形为轴对称图形.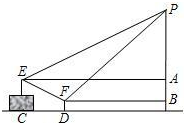 广场上有一个充满氢气的气球P,被广告条拽着悬在空中,甲乙二人分别站在E、F处,他们看气球的仰角分别为30°、45°,E点与F点的高度差AB为1米,水平距离CD为5米,FD的高度为0.5米,请问此气球有多高?(结果保留根号)
广场上有一个充满氢气的气球P,被广告条拽着悬在空中,甲乙二人分别站在E、F处,他们看气球的仰角分别为30°、45°,E点与F点的高度差AB为1米,水平距离CD为5米,FD的高度为0.5米,请问此气球有多高?(结果保留根号) 已知AB是⊙O的直径,BP是⊙O的弦,弦CD⊥AB于点F,交BP于点G,E在CD的延长线上,EP=EG.
已知AB是⊙O的直径,BP是⊙O的弦,弦CD⊥AB于点F,交BP于点G,E在CD的延长线上,EP=EG.