题目内容
3.解下列方程组或不等式,并把不等式的解集在数轴上表示出来.(1)$\left\{\begin{array}{l}{4x+y=5}\\{2x-3y=13}\end{array}\right.$;
(2)$\frac{2+x}{2}$≥$\frac{2x-1}{3}$-2.
分析 (1)先利用加减消元法求出x的值,再利用代入消元法求出y的值即可;
(2)先去分母,再去括号,移项,合并同类项,把x的系数化为1,并在数轴上表示出来即可.
解答 解:(1)$\left\{\begin{array}{l}{4x+y=5①}\\{2x-3y=13②}\end{array}\right.$,①×3+②得,14x=28,解得x=2,把x=2代入①得,8+y=5,解得y=-3,
故方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-3}\end{array}\right.$;
(2)去分母得,3(2+x)≥2(2x-1)-12,
去括号得,6+3x≥4x-2-12,
移项得,3x-4x≥-2-12-6,
合并同类项得,-x≥-20,
把x的系数化为1得,x≤20,
在数轴上表示为: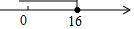 .
.
点评 本题考查的是解一元一次不等式,熟知不等式的基本性质是解答此题的关键.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
14.已知AB是⊙O内接正四边形的一边,AC是⊙O内接正六边形的一边,则∠BAC的度数为( )
| A. | 105° | B. | 150° | C. | 30° | D. | 105°或15° |
12.正方体ABCD的边长为1,点E在边AB上,BE=$\frac{1}{4}$,BF=$\frac{1}{7}$,动点P从E出发沿直线向F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角,而当碰到正方形顶点时沿入射路径反弹,当点P第一次返回E时,P所经过的路程为( )
| A. | $\sqrt{65}$ | B. | $\frac{3\sqrt{65}}{2}$ | C. | 2$\sqrt{65}$ | D. | $\frac{5\sqrt{65}}{2}$ |
 如图,六棱柱的底面边长都是5厘米,侧棱长为4厘米,则
如图,六棱柱的底面边长都是5厘米,侧棱长为4厘米,则 如图,⊙O1和⊙O2相交于A、B,C为⊙O1上一点,CA交⊙O2于D,BD交⊙O1于F,直线CF交⊙O2于E、G.
如图,⊙O1和⊙O2相交于A、B,C为⊙O1上一点,CA交⊙O2于D,BD交⊙O1于F,直线CF交⊙O2于E、G.