Question

7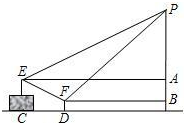．广场上有一个充满氢气的气球P，被广告条拽着悬在空中，甲乙二人分别站在E、F处，他们看气球的仰角分别为30°、45°，E点与F点的高度差AB为1米，水平距离CD为5米，FD的高度为0.5米，请问此气球有多高？（结果保留根号）

Answer 1

分析 设AP=x，先在Rt△APE中利用30的正切可表示出AE=$\sqrt{3}$x，再在Rt△BFP中利用等腰直角三角形的性质表示出BF=BP=x+1，接着利用AE=CD+BF得方程$\sqrt{3}$x=5+x+1，然后解方程求出x，最后计算PA+AB+BO即可．

解答 解：如图，
设AP=x，
在Rt△APE中，∵∠AEP=30°，
∴tan∠APE=tan30°=$\frac{AP}{AE}$=$\frac{\sqrt{3}}{3}$，
∴AE=$\sqrt{3}$x，
在Rt△BFP中，∵∠BFP=45°，
∴BF=BP=AB+AP=x+1，
∵AE=CD+BF，
∴$\sqrt{3}$x=5+x+1，解得x=3$\sqrt{3}$+3，
∴PO=PA+AB+BO=3$\sqrt{3}$+3+1+1=3$\sqrt{3}$+5．
答：此气球有高度为（3$\sqrt{3}$+5）米．

点评 本题考查了解直角三角形的应用-仰角俯角问题：仰角是向上看的视线与水平线的夹角；解决此类问题要了解角之间的关系，找到与已知和未知相关联的直角三角形．