题目内容
8.已知平行四边形ABCD的两边AB,AD的长是关于x的方程:x2+(2m-1)x+4=0的两个实根.(1)当AB=1时,平行四边形ABCD的周长是多少?
(2)当m为何值时,平行四边形ABCD是菱形?
分析 (1)由一元二次方程的根与系数的关系求出AD的长,即可得出平行四边形ABCD的周长;
(2)四边形ABCD是菱形时,AB=AD,由一元二次方程根的判别式=0即可求出m的值.
解答 解:(1)当AB=1时,
∵AB,AD的长是关于x的方程x2+(2m-1)x+4=0的两个实数根,
∴AB•AD=4,
∴AD=4,
∴?ABCD的周长=2(AB+AD)=2(1+4)=10;
(2)四边形ABCD是菱形时,AB=AD,
∵AB,AD的长是关于x的方程x2+(2m-1)x+4=0的两个实数根,
∴△=(2m-1)2-4×1×4=0,
解得:m=-1.5或m=2.5(不合题意,舍去),
∴当m=-1.5时,四边形ABCD是菱形.
点评 本题考查了菱形的判定、平行四边形的性质、一元二次方程的根与系数的关系、根的判别式;熟练掌握平行四边形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
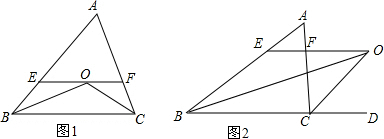
 如图,正方形ABCD的边长为2,点E是BC的中点,点F在BC的延长线上,且EF=DE,以CF为边作正方形CFGH,点H在CD边上.试说明点H是线段CD的一个黄金分割点.
如图,正方形ABCD的边长为2,点E是BC的中点,点F在BC的延长线上,且EF=DE,以CF为边作正方形CFGH,点H在CD边上.试说明点H是线段CD的一个黄金分割点.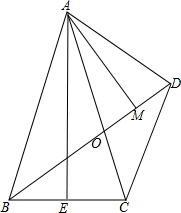 如图,△ABC中,AB=AC,AE⊥BC于E,D为△ABC外-点,且∠ABD=∠ACD,BD交AC于O,AM⊥BD于M,连AD.
如图,△ABC中,AB=AC,AE⊥BC于E,D为△ABC外-点,且∠ABD=∠ACD,BD交AC于O,AM⊥BD于M,连AD.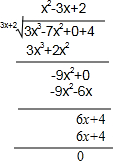 我们学过单项式除以单项式、多项式除以单项式,那么多项式除以多项式该怎么计算呢?我们可以用竖式进行演算,即先把被除式、除式按某个字母作降幂排列,并把所缺的项用零补齐,再类似数的竖式除法求出商式和余式,其中余式为0或余式的次数低于除式的次数.例如:
我们学过单项式除以单项式、多项式除以单项式,那么多项式除以多项式该怎么计算呢?我们可以用竖式进行演算,即先把被除式、除式按某个字母作降幂排列,并把所缺的项用零补齐,再类似数的竖式除法求出商式和余式,其中余式为0或余式的次数低于除式的次数.例如: 已知:线段a、h,如图,求作:等腰三角形ABC,使得其腰长为a,底边上的中线为h.
已知:线段a、h,如图,求作:等腰三角形ABC,使得其腰长为a,底边上的中线为h.