题目内容
20.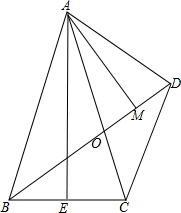 如图,△ABC中,AB=AC,AE⊥BC于E,D为△ABC外-点,且∠ABD=∠ACD,BD交AC于O,AM⊥BD于M,连AD.
如图,△ABC中,AB=AC,AE⊥BC于E,D为△ABC外-点,且∠ABD=∠ACD,BD交AC于O,AM⊥BD于M,连AD.(1)求证:∠BDC=2∠BAE
(2)求证:∠DBC+△BCD=2∠ADB
(3)求:$\frac{BD-CD}{DM}$的值.
分析 (1)根据等腰三角形的性质得到∠BAC=2∠BAE,由∠ABD=∠ACD,于是得到A,B,C,D四点共圆,根据圆周角定理即可得到结论
(2)由∠ABD=∠ACD,∠ABC=∠ACB,于是得到∠ACD+∠DBC=∠ABC=∠ACB,等量代换得到∠DBC+∠BCD=2∠ACB,根据圆周角定理得到∠ADB=∠ACB,即可得到结论;(3)在BD上截取BF=CD,证得△ABO∽△ACD,得到AF=AD,根据等腰三角形的性质得到DF=2DM,于是求得结果.
解答 解:(1)∵AB=AC,AE⊥BC于E,
∴∠BAC=2∠BAE,
∵∠ABD=∠ACD,
∴A,B,C,D四点共圆,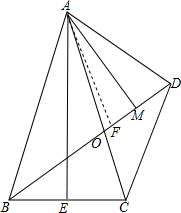
∴∠BDC=∠BAC=2∠BAE;
(2)∵∠ABD=∠ACD,∠ABC=∠ACB,
∴∠ACD+∠DBC=∠ABC=∠ACB,
∴∠DBC+∠BCD=2∠ACB,
∵A,B,C,D四点共圆,
∴∠ADB=∠ACB,
∴∠DBC+∠BCD=2∠ADB;
(3)在BD上截取BF=CD,
在△ABO与△ACD中,$\left\{\begin{array}{l}{AB=AC}\\{∠ABD=∠ACD}\\{BF=CD}\end{array}\right.$,
∴△ABO∽△ACD,
∴AF=AD,∵AM⊥DF,
∴DF=2DM,
∴$\frac{BD-CD}{DM}$=$\frac{BD-BF}{DM}$=$\frac{2DM}{DM}$=2.
点评 本题考查了相似三角形的判定和性质,四点共圆,三角形的内角和定理,等腰三角形的性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
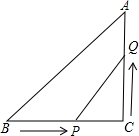 如图所示,在△ABC中,∠C=90°,BC=8cm,AC:AB=3:5,点P从点B出发沿BC向点C以2cm/s的速度移动,点Q从点C出发沿CA向点A以1cm/s的速度移动,如果P、Q分别从B、C同时出发:
如图所示,在△ABC中,∠C=90°,BC=8cm,AC:AB=3:5,点P从点B出发沿BC向点C以2cm/s的速度移动,点Q从点C出发沿CA向点A以1cm/s的速度移动,如果P、Q分别从B、C同时出发: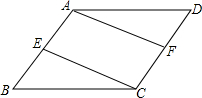 如图,在菱形ABCD中,E,F分别是AB和CD的中点,连接AF,CE.
如图,在菱形ABCD中,E,F分别是AB和CD的中点,连接AF,CE. 如图,在△ABC中,若沿EF折叠,恰好使点A落在BC上的点D处,请你说明EF⊥AD.
如图,在△ABC中,若沿EF折叠,恰好使点A落在BC上的点D处,请你说明EF⊥AD.